
創始於1999年1月16日的數學網站
更新日期:2024年10月21日
| 新增素材 | 數學燈謎 | GeoGebra | 笑話數學 | 中小學科展 | 微教學動畫 |
■ 正方形內相切兩半圓
■ 偶位數的光棍數
$111111111111=222222+333333^2$
■ 尖嘴弧壺的面積
■ 三角形重心連接頂點三等分面積
■ 圖示配方法
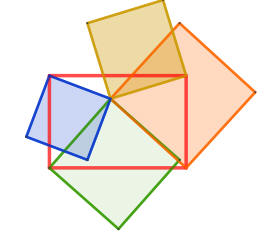
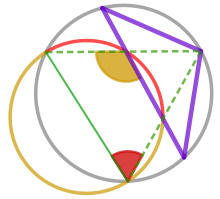
| 四個正方形面積的關係 | 圓內接四邊形對角互補的應用 |
 |
 |
|
更新日期:2024年10月21日
| 新增素材 | 數學燈謎 | GeoGebra | 笑話數學 | 中小學科展 | 微教學動畫 |
■ 正方形內相切兩半圓
■ 偶位數的光棍數 $111111111111=222222+333333^2$
■ 尖嘴弧壺的面積
■ 三角形重心連接頂點三等分面積
■ 圖示配方法
|