機率樹狀圖和二項式定理

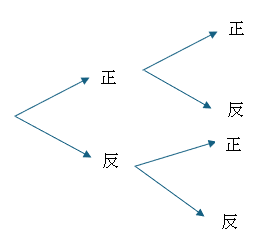
投擲一個硬幣，不是正面朝上就是反面朝上，如果試驗二次，則可能結果有 ( 正，正 )、( 正，反 )、( 反，正 )、( 反，反 )，其中 ( 正，反 )表示第一次試驗正面朝上，第二次試驗反面朝上。

如果正面朝上的機率是 p，反面朝上的機率是 q，則 p+q=1。

結果	( 正，正 )	( 正，反 )	( 反，正 )	( 反，反 )
機率	$\large p^2$	$\large pq$	$\large qp$	$\large q^2$

因為 $\large p^2+2pq+q^2=1$，所以 $\large(p+q)^2= p^2+2pq+q^2=1$。

即 $ p+q=1$， $\large\dbinom{2}{0}p^0q^{2-0}+\dbinom{2}{1}p^1q^{2-1}+\dbinom{2}{2}p^2q^{2-2}=1$。

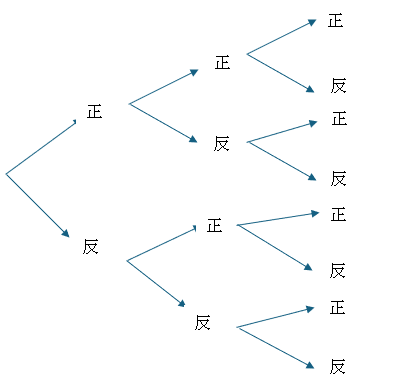
投擲一個硬幣，不是正面朝上就是反面朝上，如果試驗三次，則結果和其機率如下

結果	( 正，正，正 )	( 正，正，反 )	( 正，反，正 )	( 正，反，反 )	( 反，正，正 )	( 反，正，反 )	( 反，反，正 )	( 反，反，反 )
機率	$\large p^3$	$\large p^2q$	$\large p^2q$	$\large pq^2$	$\large p^2q$	$\large pq^2$	$\large pq^2$	$\large q^3$

因為 $\large p^3+3p^2q+3pq^2q^3=1$，所以 $\large(p+q)^3= p^3+3p^2q+3pq^2+q^3=1$。

即 $ p+q=1$， $\large\dbinom{3}{0}p^0q^{3-0}+\dbinom{3}{1}p^1q^{3-1}++\dbinom{3}{2}p^2q^{3-2}\dbinom{3}{3}+p^3q^{3-3}=1$。