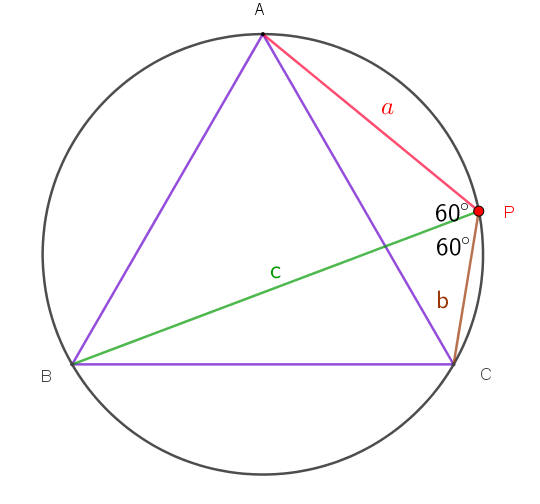
令$\overline{PA}=a$，$\overline{PC}=b$，$\overline{PB}=c$，已知∠APB=∠CPB=60°，

(1) 如果a=b，則△APB全等於△CPB(SAS或SSS)，因此∠ABP=∠CBP=30°，得∠BAP=∠BCP=90°，c=2a且c=2b，所以c=a+b。

(2) 如果a≠b，從餘弦定理可知 a²+c²-2acCos60°=b²+c²-2bcCos60°，因此a²-ac=b²-bc，即 a²-b²=ac-bc=c(a-b)，

(a+b)(a-b)=c(a-b)，得 c=a+b。

如果只要運用國中的數學知識，可以證明如下