地下停車場的限定高度

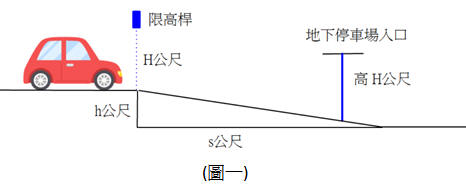
地下停車場的限高桿會標明車子安全入場的限定高度，駕駛要如何選擇限定高度，以便車子安全順利進入地下停車場？
(討論的地下停車場沒有機械車位)

如圖一，地下停車場坡道水平距離s公尺，垂直距離h公尺，目前規定$\large\frac{h}{s}$ ≦ $\large\frac{1}{6}$，即坡度不超過 16.67％，斜坡角度不超過9.46度。

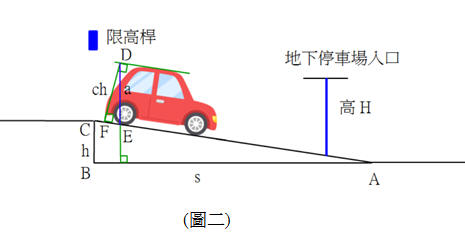
如圖二，DF⊥AC，$\vec{DE}$⊥AB。

如果車高DF=ch公尺，限高桿位置離地面高H公尺，車子欲安全順利進入地下停車場，則直角三角形DEF的DE長a不超過H，即 ch < a ≦ H。

令 AB=s公尺，BC=h公尺，則AC=$\sqrt{s^2+h^2}$ 公尺。
已知直角三角形ABC相似於直角三角形DEF，所以 a : ch = $\sqrt{s^2+h^2}$ : s， a = ch × $\large\frac{\sqrt{s^2+h^2}}{s}$。
由上述可知，車子駕駛選擇的限定高度H應該不小於 ch × $\large\frac{\sqrt{s^2+h^2}}{s}$，他的車子才可以安全進入地下停車場。

實例：

如果車高1.75公尺，地下停車場坡道的坡度是15％，車子駕駛應該選擇限高多少公尺的停車場，才能安全順利進入停車場？

因為坡度是15％，即$\large\frac{h}{s}$=$\large\frac{15}{100}$，令 s=20x，h=3x，則 a= 1.75×$\large\frac{\sqrt{(20x)^2+(3x)^2}}{20x}$ ≒ 1.77。因為 H ≧ a，所以限高桿的位置離地面不小於1.77公尺，因此車子駕駛應該選擇限高1.77公尺以上的停車場，即他最好選擇限高1.8公尺、1.9公尺、2公尺…的地下停車場。