111年學測數學A(20a)

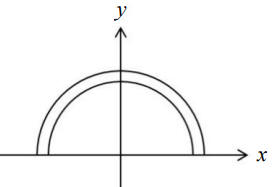
坐標平面上有一環狀區域由圓 x²+y²=3的外部與圓 x²+y²=4 的內部交集而成。某甲欲用一支長度為 1 的筆直掃描棒來掃描此環狀區域之 x 軸上方的某區域 R。他設計掃描棒黑、白兩端分別在半圓 C₁ : x²+y²=3( y ≧ 0 )、 C₂ : x²+y²=4( y ≧ 0 )上移動。開始時掃描棒黑端在點 A( $\sqrt{3}$，0) ，白端在 C₂ 的點 B。接著黑、白兩端各沿著 C₁、 C₂ 逆時針移動，直至白端碰到 C₂ 的點 B'( -2,0) 便停止掃描。

第20題︰

（承 19 題）令Ω 表示掃描棒在第一象限所掃過的區域Ω，試求 Ω的面積。