第1頁 第2頁 第3頁 第4頁 第5頁 第6頁 第7頁 第8頁 第9頁 第10頁
26.
| 適合對象︰高一 | 能力指標: 算幾不等式 | 難度指數：☆☆☆☆☆ |
|
試證︰
|
||
27.
| 適合對象︰國二 | 能力指標: 分數運算 | 難度指數：☆☆☆☆ |
|
試說明$\frac{1}{3}+\frac{3}{5}+\frac{5}{7}+\frac{7}{9}+\frac{9}{11}$最接近於哪一個整數?
|
||
$\frac{1}{3}+\frac{3}{5}+\frac{5}{7}+\frac{7}{9}+\frac{9}{11}$=
$1-\frac{2}{3}+1-\frac{2}{5}+1-\frac{2}{7}+1-\frac{2}{9}+1-\frac{2}{11}$=
$5-2(\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{9}+\frac{1}{11})$ < $5-2((\frac{1}{6}+\frac{1}{6})+(\frac{1}{12}+\frac{1}{12}+\frac{1}{12}))$ =$5-2\times\frac{7}{12}$=$3+\frac{5}{6}$
所以$\frac{1}{3}+\frac{3}{5}+\frac{5}{7}+\frac{7}{9}+\frac{9}{11}$最接近於整數4。
28.
| 適合對象︰高一 | 能力指標: 不等式 | 難度指數：☆☆☆☆☆ |
|
|
||
pq+qr+rp-2pqr-1=rp+qr-pqr-r+pq-pqr+r-1=
r(p+q-pq-1)+pq(1-r)+(r-1)=r[(p-1)+q(1-p)]+(1-r)(pq-1)=
r(p-1)(1-q)+(1-r)(pq-1)
因為r(p-1)(1-q)<0且(1-r)(pq-1)<0，所以r(p-1)(1-q)+(1-r)(pq-1)<0。
因此pq+qr+rp-2pqr-1<0，即pq+qr+rp-2pqr<1。
29.
| 適合對象︰九年級(國三) | 能力指標: 中垂線 | 難度指數：☆☆☆☆☆ |
|
|
||
|
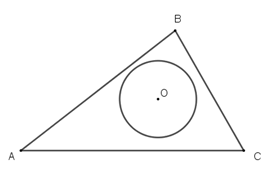
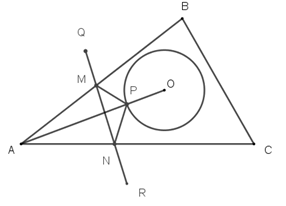
顯然，連接OA，OA和圓O的交點P，PA最短。 過P點分別作AB和AC的對稱點Q點和R點。 QR分別交AB和AC於M點和N點。 三角形PMN即為所求。
|
|
| 假設S不同於M，T不同於N。顯然三角形PST的周長=SQ+ST+TR > QR。 |
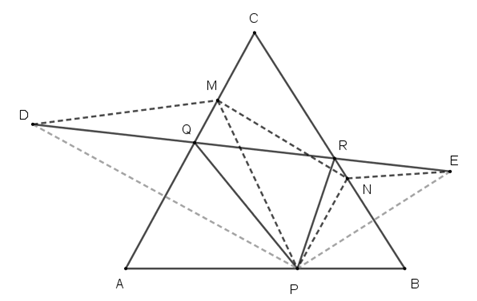
30.
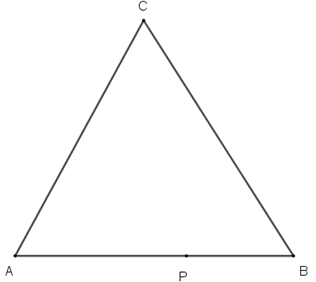
| 適合對象︰九年級(國三) | 能力指標: 中垂線 | 難度指數：☆☆☆☆☆ |
|
三角形ABC，P點是AB上任一點。試在AC和BC上取Q點和R點，使得三角形PQR的周長最小。
|
||
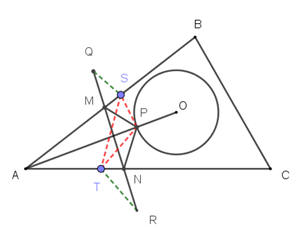
P點分別以AC和BC為對稱軸，對稱點分別是D點和E點。
連DE，分別交AC和BC於Q點和R點，三角形PQR即為所求。
假設M點在AC且M≠Q，N點在BC且N≠R，則MP=MD且NP=NE。
三角形PMN的周長=PM+MN+NP=DM+MN+NE >DE=DQ+QR+RE=三角形PQR的周長。
第1頁 第2頁 第3頁 第4頁 第5頁 第6頁 第7頁 第8頁 第9頁 第10頁
Copyright © 昌爸工作坊 all rights reserved.