如圖，圓O的半徑長6，弦CD與弦EF都垂直於直徑AB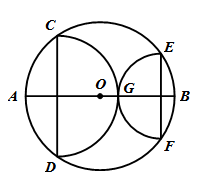
第1頁 第2頁 第3頁 第4頁 第5頁 第6頁 第7頁 第8頁 第9頁 第10頁
16.
| 適合對象:九年級 | 能力指標:圓周角，全等三角形 | 難度指數：☆☆☆☆☆ |
|
如圖，圓O的半徑長6，弦CD與弦EF都垂直於直徑AB |
||
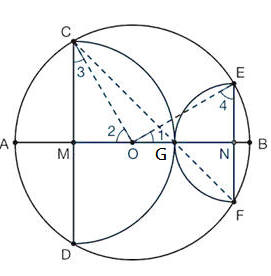
解析:
因為 ∠ CFE=45∘，所以∠ COE=90∘
因此∠1=∠3，∠2=∠4
又因為OC=OE，所以△CMO≌△ONE (ASA)
因此MO=EN(小半圓的半徑)
因為直角△CMO，CO2=CM2+MO2
因此CO2兩個半圓的面積和=(CM2π+MO2π)÷2
所以兩個半圓的面積和=62π÷2=18π
17.
| 適合對象:九年級 | 能力指標:全等三角形，相似三角形 | 難度指數：☆☆☆☆ |
|
(105學年度彰化高中科學班甄選數學試題第7題) |
||
解析:
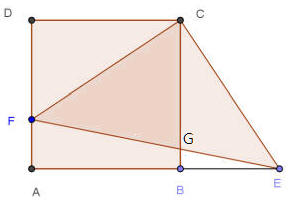令 BG
= x，BE = y，因為 BC
=16，所以 CG =16-x
因為∠FCD+∠FCB =∠ECB+∠FCB = 90∘，所以∠FCD =∠ECB，可推得∠DFC=∠BEC
又CD = CB，因此 △CDF≌△CBE(AAS全等性質)，得 DF = BE = y
FA = DA - DF =16-y
因為 GB // FA，所以 EB : EA = GB : FA，y : (16+y) = x : (16-y)
16x+xy-16y = y2
因為 △FCE的面積 = △FCG的面積 + △CEG的面積 = 200
16(16-x) + y(16-x) = 400，256-16x+16y-xy = 400，256-y2 = 400，y=12
所以
BE=12
第1頁
第2頁 第3頁 第4頁
第5頁 第6頁 第7頁
第8頁 第9頁
第10頁
Copyright © 昌爸工作坊 all rights reserved.
如圖，正方形ABCD的面積是256