疑難解析

第1頁第2頁第3頁第4頁第5頁第6頁第7頁第8頁第9頁第10頁

31.

適合對象︰國三

能力指標: 全等形

難度指數：☆☆☆☆☆

張進通許世賢教育文教基金會111學年度雲嘉南區國中數學能力競試「數學二」填充第7題

32.

適合對象︰九年級(國三)

能力指標: 全等形

難度指數：☆☆☆☆☆

等腰三角形ABC，AB=AC，∠A=20°。如果D在AC且AD=BC，則∠BDC是幾度?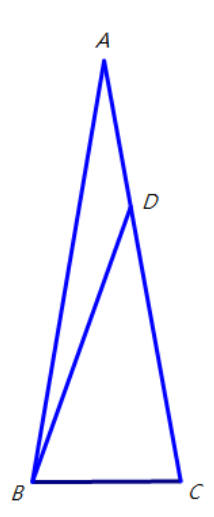

作正三角形BCE，E點在三角形ABC內.
連AE.
角∠ECB=60°，∠ACB=80°，∠ACE=(80-60)°=20°=∠BAD.

因為AD=BC=CE,，∠ACE=∠BAD且AC=BA，
所以三角形ACE全等於三角形BAD(SAS全等)

因為三角形ABE全等於ACE((SSS全等)
所以∠BAE=∠CAE=(20/2)°=10°=∠ABD

∠BDC=∠BAD+∠ABD(外角定理)
=(20+10)°=30°

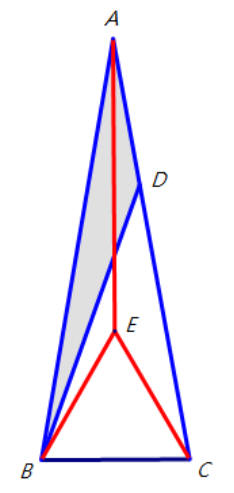33.

適合對象︰國三

能力指標: 圓，相似形

難度指數：☆☆☆☆☆

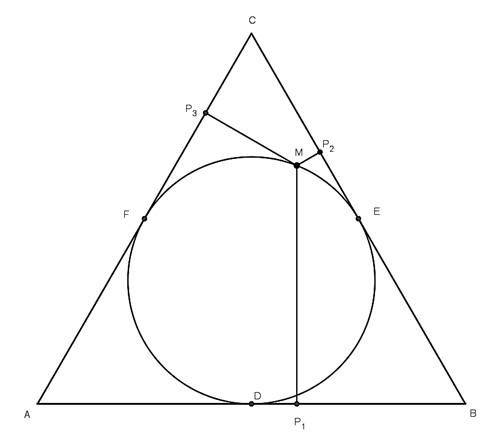
正三角形ABC內切圓切點分別是D點、E點、F點。 $\widehat{EF}$ 弧上一點M正三角形ABC三邊作垂線，垂足分別是P₁試說明 $\sqrt{p}=\sqrt{q}+\sqrt{r}$

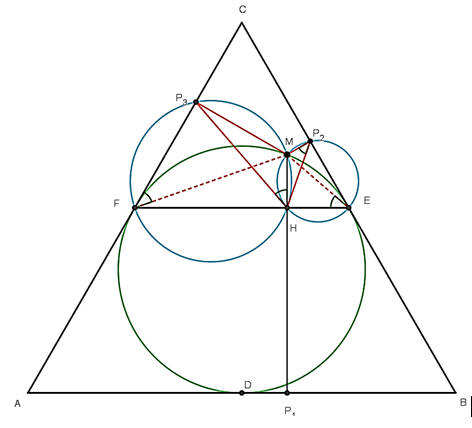連EF，

MP₁和EF相交於H點。
因為E點和F點是中點，且EF//AB，

所以正三角形CEF的高=HP₁。

因為正三角形CEF的高=MH+MP₂+MP₃，所以HP₁=MH+MP₂+MP₃_。
因此MP₁=MH+HP₁=2MH+MP₂+MP₃，即 p=2MH+q+r....(1)。

因為M、H、E、P₂四點共圓，所以∠MP₂H=∠MEH(對同弧 $\widehat{MH}$ )
因為M、H、F、P₃四點共圓，所以∠MHP₃=∠MFP₃(對同弧 $\widehat{MP_3}$ )
因為正三角形ABC內切圓，弦切角∠P₃FM=∠MEF(圓周角)=∠MEH，所以∠MHP₃=∠MP₂H。
同理可證∠MP₃H=∠MHP₂。
因此三角形MP₃H相似於三角形MHP₂。
因為 MH︰MP₂=MP₃︰MH，所以MH²=MP₂×MP₃=qr
因此= $\sqrt{qr}$ ....代入(1)
p=2 $\sqrt{qr}$ +q+r=( $\sqrt{q}+\sqrt{r}$ )²
所以 $\sqrt{p}=\sqrt{q}+\sqrt{r}$ 得證

第1頁第2頁第3頁第4頁第5頁第6頁第7頁第8頁第9頁第10頁