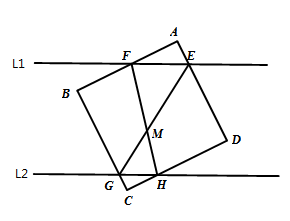
如圖，正方形ABCD，L1
// L2，正方形ABCD的四邊分別與L1和L2相交於E、F、G、H，
且與FH相交於M，若正方形ABCD的邊長與平行線L1、L2的距離相等。
(1).試說明平分∠BFE。
(2).試求∠FME的度數？
第1頁 第2頁 第3頁 第4頁 第5頁 第6頁 第7頁 第8頁 第9頁 第10頁
10.
| 對象：九年級 | 能力：平行性質，全等三角形 | 難度指數：☆☆☆☆☆ |
|
|
||
解析:
(1)
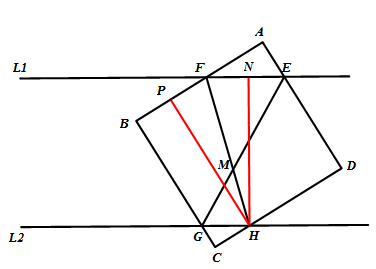
過H作HP⊥AB，作HN⊥L1，
因為正方形ABCD的邊長與平行線L1、L2的距離相等，所以HP＝HN。
因為∠P＝∠N＝90∘，HF＝HF，HM＝HN，所以△HPF≌△HNF
(RHS性質)，
因此，∠PFH＝∠NFH，即平分∠BFE。
(2)
同理可證FG平分∠FED，即∠FEG＝∠DEG。
因為∠BFE和∠DEF都是△AFE的外角，所以∠BFE+∠DEF＝180∘+∠A＝270∘。
在△EFM中，∠E+∠F＝(∠BFE+∠DEF)÷2＝135∘，因此
∠FME＝(180−135)∘＝45∘。
11.
| 對象：九年級 | 能力：重心 | 難度指數：☆☆☆☆ |
|
|
||
解析：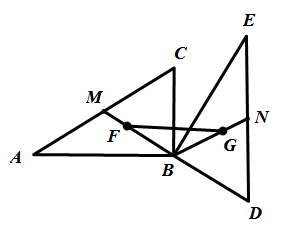
因為F與G分別是△ABC與△EBD的重心，所以M與N分別是AC與DE的中點。
因為∠ABC＝∠EBD＝90∘，且M與N分別是AC與DE的中點，所以MC＝MB＝5且NE＝NB＝5，因此
∠C＝∠MBC且∠E＝∠NBE。
因為直角△ABC全等於直角△EBD，，，所以∠C＝∠D。
因為∠D+∠E＝90∘，所以∠C+∠E＝90∘，因此∠MBC+∠NBE＝90∘。
因為∠FBG＝∠MBC+∠CBE+∠NBE＝(90+30)∘＝120∘。
因為△FBG中，BF＝5×2/3＝10/3，BG＝5×2/3＝10/3，∠FBG＝120∘所以FG＝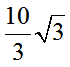
。
12.
| 對象：九年級 | 能力：相似形 | 難度指數：☆☆☆☆ |
|
|
||
解析:
(1)
直線DF交直線AB於G，
因為∠GAE＝∠DCE，AE＝CE，∠AEG＝∠CED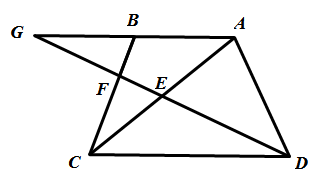
所以△GAE≌△DCE (ASA)
因此 GA＝DC
又CD＝2AB
△AED面積＝△CED面積＝△ABC面積
因為△GBF~△DFC，△GBF面積：△DFC面積＝1：4
(3)
令四邊形ABFE的面積＝a，△AED面積＝△CED面積＝△ABC面積＝x
則△EFC面積＝x−a
因為△GBF面積：△DFC面積＝1：4
所以△GBF面積＝△DFC面積/4＝(x−a+x)/4
因為△GAE≌△DCE
所以[(x−a+x)/4] + a＝x
3a＝2x
a：x＝2：3
四邊形ABFE的面積與△CDE的面積比＝2：3
第1頁 第2頁 第3頁 第4頁 第5頁 第6頁 第7頁 第8頁 第9頁 第10頁
Copyright ©昌爸工作坊 all rights reserved.
右圖，直角△