利用算幾不等式證明

$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}$  ≧ $\large\frac{3}{2}$

算術平均數大於等於幾何平均數

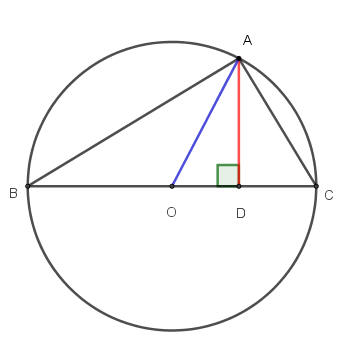
如附圖，圓O的直徑是BC，D點是BC上動點，過D點作垂線交圓周於A點。
則三角形ABC是直角三角形且AD²=DB × DC  (母子相似性質)。

因為 OA =$\frac{\overline{DB}+\overline{DC}}{2}$ ，AD=$\small\sqrt{\overline{DB}\times\overline{DC}}$。

顯然 OA  ≧  OD ，所以 $\frac{\overline{DB}+\overline{DC}}{2}$ ≧ $\small\sqrt{\overline{DB}\times\overline{DC}}$。

性質1︰「 a>0，b>0，c>0，則 ( $\small a+b+c$ )( $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$ ) ≧ 9 」

( $\small a+b+c$ )( $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$ )

=( $\frac{a}{a}+\frac{a}{b}+\frac{a}{c}$ )$+$( $\frac{b}{a}+\frac{b}{b}+\frac{b}{c}$ )$+$( $\frac{c}{a}+\frac{c}{b}+\frac{c}{c}$ )

= 3$+$( $\frac{a}{b}+\frac{b}{a}$ )$+$( $\frac{b}{c}+\frac{c}{b}$ )$+$( $\frac{c}{a}+\frac{a}{c}$ )

≧  3$+$ 2$\sqrt{\frac{a}{b}\times\frac{b}{a}}$$+$ 2$\sqrt{\frac{b}{c}\times\frac{c}{b}}$ $+$ 2$\sqrt{\frac{c}{a}\times\frac{a}{c}}$ = 9

所以 $\small(a+b+c)$($\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$)  ≧ 9

性質2︰「 a>0，b>0，c>0，則 $\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}$  ≧  $\large\frac{3}{2}$ 」

3$+$$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}$

= $\frac{a+b+c}{b+c}+\frac{b+c+a}{c+a}+\frac{c+a+b}{a+b}$

= ($\small a+b+c$)($\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}$ )

= $\frac{1}{2}$×2($\small a+b+c$)($\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}$ )

= $\frac{1}{2}$×[($\small b+c$)+($\small c+a$)+($\small a+b$)]($\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}$ )  

≧ $\frac{1}{2}$×9 = $\large\frac{9}{2}$，因此得

( 3$+$$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}$ )-3 ≧  $\large\frac{9}{2}$-3，即

$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}$ ≧  $\large\frac{3}{2}$

性質3︰「 a>0，b>0，c>0，則 $\frac{a+b}{c}+\frac{b+c}{a}+\frac{c+a}{b}$  ≧  6 」

 $\frac{a+b}{c}+\frac{b+c}{a}+\frac{c+a}{b}$

= ( $\frac{a}{b}+\frac{b}{a}$ )$+$( $\frac{b}{c}+\frac{c}{b}$ )$+$( $\frac{c}{a}+\frac{a}{c}$ )

≧  2$\sqrt{\frac{a}{b}\times\frac{b}{a}}$$+$ 2$\sqrt{\frac{b}{c}\times\frac{c}{b}}$ $+$ 2$\sqrt{\frac{c}{a}\times\frac{a}{c}}$ = 6

Copyright ©昌爸工作坊 All Rights Reserved.