日 期
題 目
題 解
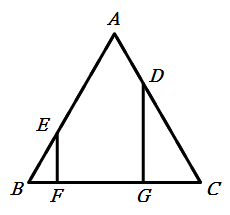 右圖是正三角形ABC,AE長是AD的2倍。若
EF⊥BC,DG⊥BC,已知
FG =
9,則AE長是多少﹖
右圖是正三角形ABC,AE長是AD的2倍。若
EF⊥BC,DG⊥BC,已知
FG =
9,則AE長是多少﹖
令AE=x,AB=a,則
BE=a-x,AD=x/2,CD=a-(x/2)
因為BF=(a-x)/2且CG=[a-(x/2)]/2
所以(a-x)/2 + 9 + [a-(x/2)]/2=a
a-x+18+a-(x/2)=2a
3x/2=18,x=12 ,所以AE長是12
(25)
屏師(50)級賴清雄,黃小偉 ,苦力爸,陳裕仁, 胡城瑋( 桃園私立六和高中),小河壩,周景佑 (彰化市),佩恩 ,
朱慶仁,vinskman(香港) ,p889013 ,Lim BK ,李昌明 ,徐宏全, 蕭偉智(新北市文山國中),洪偉誠 (高雄),
徐暉庭(振聲中學國二平),dazzmoon1 ,馮甯,周弘宇(桃園縣),陳黎, 林旭(員林 大同國中 330 ),温錦隆老師(彰化縣鹿港鎮新興國小) ,楊承澔,郭順興(興桑)
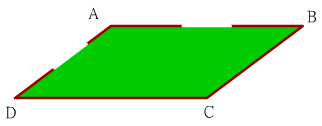
如圖,一塊平行四邊形草地,∠A=150∘,如果要使用籬笆圍住四周,但是要在AB和AD邊各留1公尺的出入口,已知使用的籬笆總長是22公尺,則這塊平行四邊形草地的最大面積是多少平方公尺﹖
依題意 x+y+(x-1)+(y-1)=22
因此x+y=12,y=12-x
因為∠B=30∘,所以平行四邊形ABCD的面積=(x/2)y=
(x/2)(12-x)=(-1/2)(x2-12x+36)+18=(-1/2)(x-6)2+18
≦18
因此平行四邊形草地的最大面積是18平方公尺
(20)
周景佑,小河壩
,咖啡大,黃小偉,賴清雄(屏師50級),陳裕仁
,p889013,
李昌明,朱慶仁,
小魚老師(外埔國中),dazzmoon1
,周弘宇(桃園縣),
李家瑞,vinskman(香港),温錦隆老師(彰化縣新興國小),Shu-Chuan
Chiu
,
郭進壽
,洪偉誠
(高雄),丁
浩文
,郭順興(興桑)
雅貞由1~2n中(n是正整數),任意選取n個數,並由大而小排列成a1、a2、a3、…、an-1、an。健雄則從雅貞所選剩下的n個數,由小而大排列成b1、b2、b3、bn-1、bn。若將兩個數列的n個同項差(
| an-bn | )相加,結果是729,例如︰
|a1-b1|+|
a2-b2|+…+|an-1-bn-1|+|an-bn|=729,則n=?
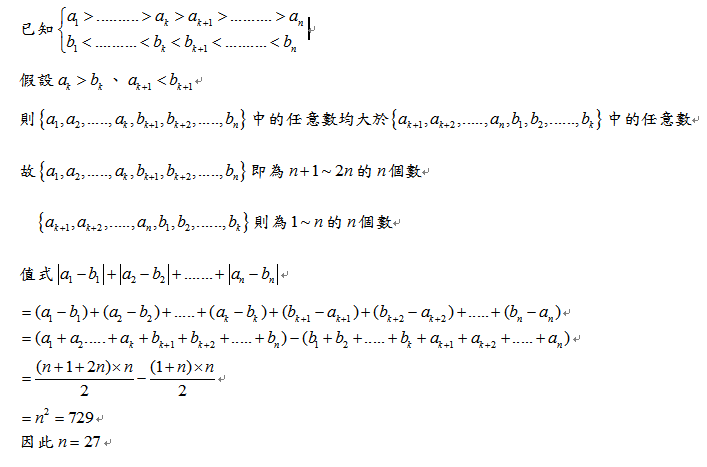
--小明--
(17)
小明,陳裕仁,小魚老師(台中 外埔國中), p889013 ,郭進壽, 黃小偉(高雄),朱慶仁,周景佑,小河壩,vinskman(香港),蕭偉智(新北市文山國中),dazzmoon1, boonkwang (马来西亚) ,Kohleth Chia ,温錦隆老師(彰化縣新興國小) ,周弘宇(桃園縣),薑汁咖啡 (江翠國小六年級)
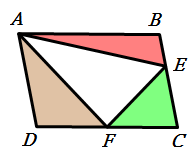 平行四邊形ABCD,F是CD的中點,E是BC上一點。若△ABE面積=a,△ECF面積=b,△ADF面積=c,試寫出a、b、c的關係式﹖
平行四邊形ABCD,F是CD的中點,E是BC上一點。若△ABE面積=a,△ECF面積=b,△ADF面積=c,試寫出a、b、c的關係式﹖
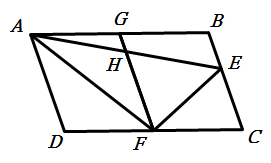 作
FG//AD
作
FG//AD
△AGH=a/4,GHEB=3a/4,
△AFH=△EFH
△ADF+△AGH=△ECF+GHEB
c+a/4=b+3a/4
4c+a=4b+3a
a=2c-2b
(19)
陳裕仁
,小魚老師(外埔國中),朱慶仁
,高雄黃小偉,小河壩
,温錦隆老師(彰化縣新興國小),咖啡大,李昌明,dazzmoonl,黃煌文,p889013,
周弘宇(桃園縣),戴坤邦老師,林旭(大同國中2年30班),ksming1.tw
,
賴宥辰,
丁浩文,郭順興(興桑)
,李家瑞
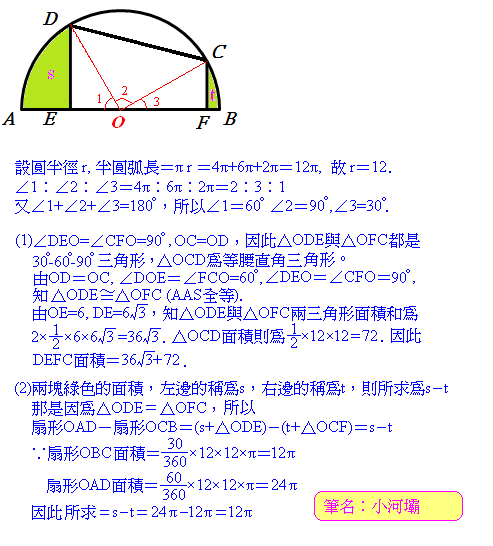
如附圖,AB是半圓的直徑,DE和CF都垂直於AB,E、F都是垂足。若AD弧長4π,DC弧長6π,CB弧長2π,則
(1)四邊形DEFC的面積為何﹖
(2)圖中兩塊綠色區域的面積相差多少﹖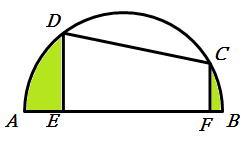
成功解題名單
(18)
周景佑,陳裕仁,p889013,李昌明,dazzmoon1,小河壩,chia hsiung cheng
,溫錦隆(彰化縣新興國小教師)
,許維縈(高雄市復華中學國中部),郭順興(興桑),周弘宇(桃園縣),蔡孟弘,王瑀謙(高雄小王子),蔡子暘
,丁浩文,陳瑞枝(桃園),朱慶仁,林群雄(高雄市東光國小)


(48)
周景佑
(彰化市),陳裕仁,雲林的阿如,王瑀謙(高雄小王子),p889013,林旭(彰化縣大同國中
2年30班) ,吳幸真(高雄),蔡孟弘,vinskman(香港),曾慶珊
,dazzmoon1
,朱慶仁,小河壩,溫錦隆老師(彰化縣新興國小),
王彥筑(彰化縣鹿港國中三年級),李昌明,周宗本,員林鎮嚕嚕咪,許維縈(高雄市復華中學國中部),洪韻涵(曉明女中),張鈞棨(杉林國中),蔡子暘,
吳岳曄(彰化縣立大同國中),
黃薏珊(彰化縣立大同國中二年三十班),楊漢,鄭毅老師(屏東市)
,
黃斌斌(歸仁國中)
,文種慧老師(雲林縣元長國中),
邱淑娟,鄭揚,賴清雄(屏師50級),林群雄(高雄市東光國小輔導主任),陳瑞枝(桃園)
,ksming1.tw,
賴宥辰 (彰化縣大同國中),郭進壽
,戴坤邦
,Vinci
Ho (香港),林世勳老師,楊承澔(秀峰高中國中部901)
,Breeze
Wu ,Huang
Ji_Chiang ,程德翔(新北市新泰國中904),靖兒(華興高級中學國中部八年級)
,Bryan
Hsieh ,莊佳潔(新竹縣博愛國中),郭順興(興桑)
,
方淑玲(建興國中)
如圖,BA切圓O於A點,BD
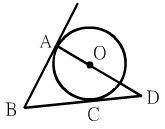
AD與圓O相交於E點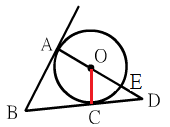
令DE=x,CD=y
因為△ABD~△COD
BD:OD=AB:CO
所以(4+y):(3+x)=4:3
,得 4x=3y
....(1)
又AD:CD=AB:CO
所以(6+x):y=4:3,得
18+3x=4y...(2)
解(1)(2)得 x=216/28, y=72/7
因此CD長=72/7
--台南市建興國中 方淑玲--
(36):
吳幸真(高雄),桃園小賴,vinskman(香港),周景佑,陳裕仁,戴坤邦,王瑀謙(高雄小王子),小河壩
(連威翔),
黃斌斌老師(台南市立歸仁國中),李昌明,chia
hsiung cheng,
溫錦隆老師(彰化縣新興國小),莊祐國教師(桃園縣立大溪國中),蕭偉智(新北市文山國中),周弘宇(桃園縣),方淑玲(台南市建興國中),賴宥辰(彰化縣大同國中),文種慧,阿如(雲林),Bryan(岡山),洪偉誠(高雄),施承祐(彰化縣鹿港國中),楊漢,嚕嚕咪(員林鎮),邱忠呈老師(高雄市立福誠高中)
,Christian
Yeh,dazzmoon1
,洪韻涵(台中市私立曉明女中三年級),安瑟斯老師(宇勝文教),張鈞棨(高雄市杉林國中),Chaun
R.Seng
,黃老師
quark,p889013,
An4976887
,陳瑞枝(桃園),楊承澔(
秀峰高中/國中部901)
如圖,正△ABC,AE:BE=1:2,BD:DC=1:2,
AD和CE相交於F點,則△AEF和△CDF的面積比=﹖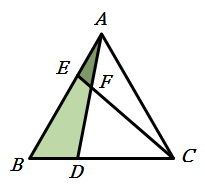
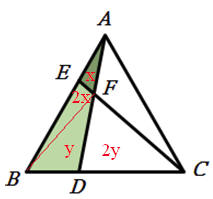 AE:BE=1:2,如果△AEF面積=x,則△BEF面積=2x。
AE:BE=1:2,如果△AEF面積=x,則△BEF面積=2x。
BD:DC=1:2,如果△BDF面積=y,則△CDF面積=2y。
因為3△ABD=△ABC,3△CBE=2△ABC,
所以 6△ABD=3△CBE,即2△ABD=△CBE,
因此 2(3x+y)=2x+3y,
4x=y,即x:y=1:4,x:2y=1:8
所以△AEF和△CDF的面積比=1:8
---蕭偉智(新北市文山國中)---
(30):
△BFC和△DEF的面積相差6.4,則△ADE的面積為何﹖
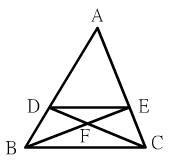

~郭順興(興桑)~
(32):
李昌明,嚕嚕咪(員林),周景佑(彰化),pobylin,steven
chen (香港),James(阿湛),朱慶仁,小河壩 ,陳裕仁,郭順興(興桑),丁浩文,溫錦隆老師
(彰化縣新興國小),楊漢丁,邱創毅,chc6565,周弘宇(桃園縣),敬雅棠(台中市私立曉明女中國中部三年級),dazzmoon1
,賴宥辰 ,vinskman(香港),桃園小賴 ,p889013 ,蔡子暘
,邱淑娟(新竹縣芎林鄉),詹為仁(彰化縣永靖國中),沙怡伶,鄭毅(高雄),高雄小王子,蕭偉智,楊承澔(新北市秀峰高中國中部901),洪偉誠(高雄),曾懿