日 期
題 目
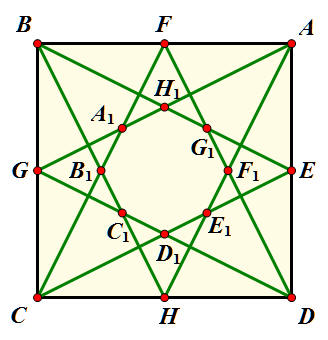
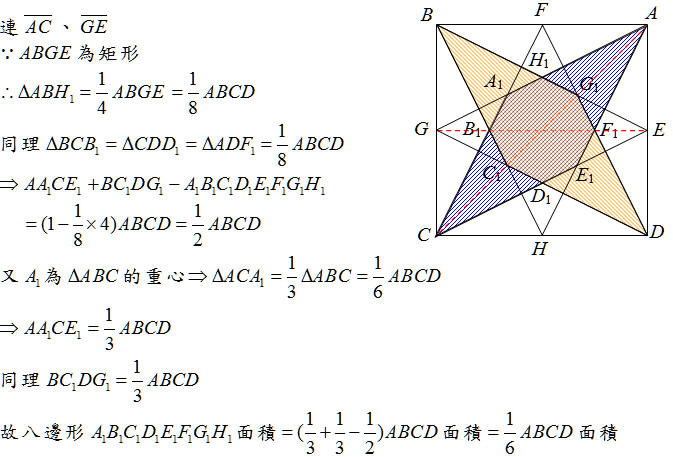
正方形ABCD,其中 E、F、G、H是各邊的中點。每一邊中點與其對邊的兩個頂點連成線段,當中線段交點的8個點,包括A1、B1、C1、D1、E1、F1、G1、H1,連接成八邊形A1B1C1D1E1F1G1H1。
試說明:八邊形A1B1C1D1E1F1G1H1的面積是正方形ABCD的
![]()
~ chang9999 ~
( 13名 )
張朗聰
chang9999
小河壩
尤銓譽
Navi Lg(香港)
周弘宇
傅強 (C.Fu)
傅遠新 (新竹實驗高中)
吳東陵
文種慧
ㄚ福 (彰化縣大同國中)
郭順興(興桑)
連啟竣
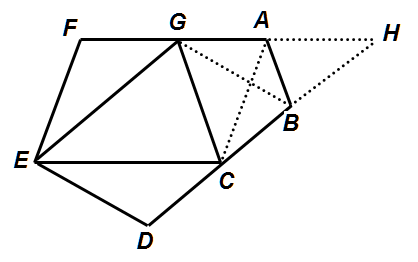
如圖,AF = CE且AF
//
CE,GE = BD且GE
//
BD,G點在 AF上,C點在BD上,且AB // GC。
試說明:
AG ×
CD = GF ×
BC
。
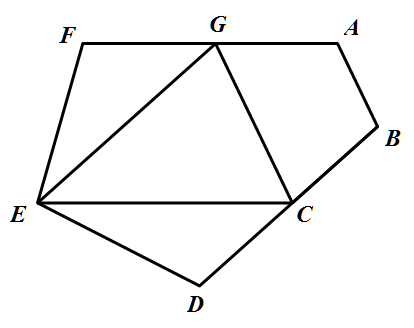
解法二:
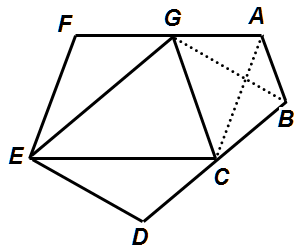
連接 BG和AC。
∵
AF
=
CE
且
AF
//
CE ∴ACEF
為平行四邊形
∵
GE
=
BD
且
GE
//
BD∴BDEG
為平行四邊形
∵ AB // GC ∴ ∆AGC = ∆BCG (同底等高) 。
∵∆AGC
+ ∆EFG = ∆CEG = ∆BCG + ∆CDE ,
已知
∆AGC = ∆BCG,
∴
∆EFG = ∆CDE
。
h1是
∆AGC 與
∆EFG分別以
AG
、
FG 為底的高。
h2是 ∆BCG
與
∆CDE分別以
BC
、CD
為底的高。
∵
∆AGC = ∆BCG 且
∆EFG = ∆CDE
∴
h1 ×
AG = h2
×
BC,
h1 ×
FG = h2
×
CD
所以
AG
:
BC =
h2:
h1
,
FG
:
CD =
h2:
h1
得 AG : BC = FG : CD ,AG x CD = GF x BC 。
~ㄚ福(彰化縣大同國中)~
解法一:
如圖,延長FA與DB,並相交於H點。
作輔助線BG與AC
。
因為ACEF與HCEG皆為平行四邊形,AF=CE,GH=EC,所以FA=GH,可知HA=GF
,同理可知 HB=CD
。
因為 AB
// GC 由平行線截成比例性質可得
AG : HA
= BC : HB 置換成AG
: GF = BC
: CD
,因此 AG x
CD = GF x BC
。
~ 文種慧~
成功解題名單
( 16名 )
wei kang lin,陳瑞柱
,洪偉誠,ㄚ福(彰化縣大同國中) ,李昌明 ,楊漢 ,文種慧,
周弘宇(桃園市),Catherine,施韋嘉
,莊勝傑 ,傅強(C.Fu) ,陳湋昱 ,朱慶仁 ,連威翔
,張朗聰