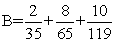|
時期 |
題目 |
解題 |
|
071102~071112
|
自然數刪去2的倍數,再刪去3的倍數,最後又刪去5的倍數。留下了1,7,11,13,..........,試問在這一序列數當中的第720個數是多少?
解題成功者:
李昌明,陳麗旭,胡軍,蔡伯仁,
陳彥螢(北縣新泰國中),Frank
Lin,
chun fuk chor(香港),montana_chen,吳
孝仁,曾耀賢(北縣新泰國中),黃柏諺,leanne(南縣文賢國中),顏嘉佑(北縣大同國小) |
[2,3,5]=30,
從自然數中刪去2的倍數,再刪去3的倍數,最後又刪去5的倍數
1~30 ,留下了 1, 7,11,13,17,19,23,29
31~60 ,留下了31,37,41,43,47,49,53,59
61~90 ,留下了61,67,71,73,77,79,83,89
………………
每一區段都有8個數,而且
每一區段的最後一個數分別是29,59,89...,其相鄰兩數相差30....(1)
因為720÷8=90………0
所以求數列(1)的第90項
即29+30×(90-1)=2699..........ANS
|
|
071019~071029 |
試計算求
9816
10 的十位數字?
解題成功者:
李昌明,chun
fuk chor (香港),
蔡伯仁,蔡棋美,顏嘉佑(北縣大同國小),
游壹傑,陳彥螢(北縣新泰國中),
王維德,montana_chen,pong,
曾耀賢(北縣新泰國中)
|
解法1:

解法2 :
因為題目是求9816^10的十位數字,
因此只需考慮16的次方,觀察其十位數字的變化規則,
16^1的後二位數字為16,十位數字為1
16^2的後二位數字為56,十位數字為5
16^3的後二位數字為96,十位數字為9
16^4的後二位數字為36,十位數字為3
16^5的後二位數字為76,十位數字為7
16^6的後二位數字為16,十位數字為1
由此可知9816的次方的十位數字為1, 5 ,9, 3, 7 循環變化,因為10/5=2......0,所以9816^10的十位數字為7
|
|
071006~071012 |
計算(320+18×318)2-2×341,並以指數式表示其結果?
解題成功者:
林方蜜,╰★拈花〥惹草♂╮
,李昌明,蔡伯仁,陳永和,超級賽亞人,林庭暘,胡育淳,林美美,NG LOK TING ,lili,劉仁銘,張文田,gohn
gohnc,李家瑞 |
(320+18×318)2-2×341
=(320+2×32×318)2-2×341
=[320(1+2)]2-2×341
=(321)2-2×341
=342-2×341
=341(3-2)=341
MeiTing ,陳佩頤(南縣文賢),胡軍,陳彥螢(新泰),永興,taiwan.allergy
,陳興宏,迷漾〃洨楓☆ ,chun fuk chor (香港),姜蕙芳,pong.
|
|
070928~071005 |
一款計算機會自動以四捨五入法取近似值至整數。例如:計算 (20÷ 3)×4
時,因為 20 ÷3 會取近似值至整數7,因此最後答案會是28。彥螢使用這款計算機來計算 (200
÷n)×n ,其中n 是小於201的正整數。那麼彥螢所得的答案共有幾個不同的可能值? |
解題成功者:李昌明(下載題解) |
|
070916~070927 |
有一個直徑 40 公尺的摩天輪垂直立於地面,旋轉一 圈費時 10 分鐘,淳惠搭乘摩天輪,當高度距地面 30
公尺以上時,她可看見 101 大樓,若淳惠在摩天輪上旋轉一圈,她有多久的時間可以看見 101 大樓?
|
弦到圓心的距離為10公尺,圓之半徑為20公尺,依30-60-90,30度所對的邊為斜邊的一半,得知:30公尺以上之高度所夾之圓心角為120度,繞一圈所需之時間為10分,故看得到101大樓之時間應為10分*120/360=10/3分鐘=3分20秒
解題成功者:
李昌明 ,林美美 ,曹家駿 ,阿庭 ,chun fuk chor ,
pong ,陳華駿 , J.J.Lee , 蔡伯仁 ,(720)陳彥螢
|
|
070909~070915 |
由鐘面12點開始逆時鐘方向記數,第一圈12點記為 0,11點記為 - 1,10點記為 - 2,9點記為 - 3,依此類推
1點記為 - 11。進入第二圈時,12點記為 - 12,11點記為 - 13,10點記為 - 14,9點記為 - 15,依此類推1點記為
- 23。進入第三、四、五圈.......皆循上述規律接續記數,試問幾點表示 「- 200」?
|
各整點記數的絕對值除以12的餘數具有規律,| -200 |和| -8
|對12同餘,12+(-8)=4,所以是4點。
解題成功者:
李昌明, 小通.,720陳彥螢,
Brian Lee,林美美, J.J.Lee ,
蔡伯仁, 余東哲,林雪娟
|
|
070821~070908 |
一幢100層樓高的大廈,因升降梯出狀況,每次只能上升7層樓或下降4層樓。若阿輝在第49層樓且堅持要搭這座升降梯到達第51層樓,則阿輝搭升降梯上上下下
所經過的樓層,最少共幾層?
|
假設升降梯上升x次,下降y次,依題意
7x-4y=2,
x=(4y+2)/7是正整數,且y是正整數,y越小則x越小,所以取 (x,y)=(2,3),因此降梯上上下下
至少經過7×2+4×3=26層。
解題成功者:
J.J.Lee , 蔡伯仁
,余東哲 ,hiu tung lui ,yy6752 ,李昌明 ,montana_chen ,楊子徵 ,
葉子 ,Rock Chen ,張哲瑋 ,林雪娟 ,蔡仲傑 ,燕仔 ,jc ,吳孝仁 ,sck ,彭永興 ,pong ,Aaron
,林美美,720陳彥螢
|
|
070814~070819 |
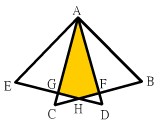 全等的正△ABC和正△ADE,相交於F點、G點、H點,且EG=DG。若DE=6,則四邊形AGHF面積=? 全等的正△ABC和正△ADE,相交於F點、G點、H點,且EG=DG。若DE=6,則四邊形AGHF面積=?
解題成功者:
J.J.Lee, montana_chen, 蔡柏仁,minmin,
余東哲,李昌明
|
AG⊥ED且AF⊥BC,
△GCH和△FDH中∠C=∠D= 60∘,
∠GHC=∠FHD= 30∘。
AG=AF
= 3√3,GC=FD
= 6-3√3,
GH=FH
= √3(6-3√3)=
6√3-9
所以 AGHF的面積=△GCH×2=
(3√3)(6√3-9)=54-27√3
|
|
070804~070811 |
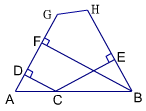 右圖,∠GAB=∠HBA,CD和BF都垂直於AG,CE垂直於HB。若BF=6,CE=4,則CD=? 右圖,∠GAB=∠HBA,CD和BF都垂直於AG,CE垂直於HB。若BF=6,CE=4,則CD=?
解題成功者:
李昌明, Brian Lee, minmin, 蔡伯仁,
rueybin, 小通, jameslee, 睿仁,
montana_chen, bohn_gohn, jjleec, GBF,
sck, 龍大俠 |
分別延長AG和BH,且相交於M點。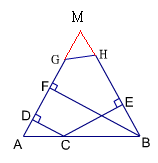
∵∠A=∠B,∴△ABM是等腰三角形,因此AM=BM。
∵△ABM面積=△ACM面積+△BCM面積
∴AM×BF=AM×CD+BM×CE,因此BF=CD+CE,CD=6-4=2。
|
|
070722~070802 |
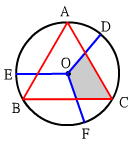
圓O是正△ABC的外接圓,半徑是6。∠DOE=∠EOF=∠FOD,試求左圖中灰色區域的面積?
解題成功者:
李嘉倫, Ping & Gary , montana_chen ,
pong , 龍大俠 , 璿仁 , 李昌明 ,
蔡伯仁 ,幻月之翼 , 蔡旻翰 ,黃金義
|
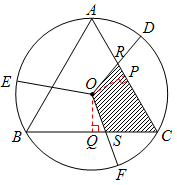 
(以上是"李昌明"的作法) |
|
070713~070720 |
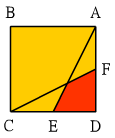 正方形ABCD的每一邊長都是6,E點和F點分別是CD和AD的中點,試求圖中紅色區域的面積? 正方形ABCD的每一邊長都是6,E點和F點分別是CD和AD的中點,試求圖中紅色區域的面積? |
連接線段AC並設AE,CF相交於O,則點O為△ACD的重心
因為三中線將三角形面積六等份,所以紅色區域面積=△ACD的面積×2/6=2/6×1/2×ABCD的面積=
6
解題成功者:
李昌明 , 蔡伯仁 , amouliu ,
橘子皮 ,trudyyeh , kill3kk , 李嘉倫 , 瑞bjo4 ,montana_chen , 張武龍 , J.J.Lee
, 豆花 ,
李sharock
, Peter蔣 , pong , BigJerry
|
|
070629~070711 |
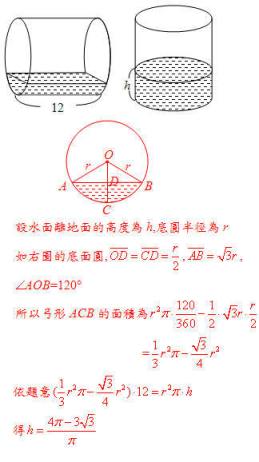
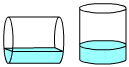 圓柱體柱高12公分,若將它平放在地面並注入一些水(左圖),
使得水面離地面的高度是底圓半徑的一半。若將它豎立起來(右圖),試求水面離地面的高度? 圓柱體柱高12公分,若將它平放在地面並注入一些水(左圖),
使得水面離地面的高度是底圓半徑的一半。若將它豎立起來(右圖),試求水面離地面的高度?
解題成功者:
李昌明, gohn gohn , jerry,
蔡伯仁, montana_chen , J.J.Lee,
Peter蔣, BigJerry
|
 |
|
070612~070621 |
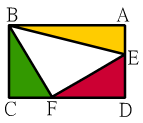 E點和F點分別在長方形ABCD的AD和DC邊上,使得△ABE面積=△BCF面積=△FDE面積,試求 E點和F點分別在長方形ABCD的AD和DC邊上,使得△ABE面積=△BCF面積=△FDE面積,試求
(1). DF÷CF的值?
(2). DE÷AE的值?
(DF>CF且DE>AE) |
令 DF/CF
= r >1,
設CF=x, ,ED=y,則 FD=xr
又因為△BCF面積=△FDE面積
所以CB=yr.
AB=x(r+1) AE=y(r-1)
又△ABE面積=△FDE面積
所以xy(r+1)(r-1)=xyr
即 r^2-r-1=0, r=(1+√5)/2
所以 DF/CF = r = (1+√5)/2
且 DE/AE = 1/(r-1) = (1+√5)/2
解題成功者:郭宗彥,Peter蔣,蔡伯仁,
李昌明,montana_chen,BigJerry |
|
070602~070608 |
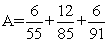 , ,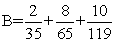
除了"通分"化簡A、B之外,試想想其他方法來比較A、B的大小?
|
A=6/55+12/85+6/91
=6/(5×11)+12/(5×17)+6/(7×13)
=1/5-1/11+1/5-1/17+1/7-1/13
=(1/5+1/5-1/17+1/7-1/13)-1/11
B=2/35+8/65+10/119
=2/(5×7)+8/(5×13)+10/(7×17)
=1/5-1/7+1/5-1/13+1/7-1/17
=(1/5+1/5-1/17+1/7-1/13)-1/7
∵ 1/11<1/7 ∴A>B
解題成功者:李昌明,天才阿張,蔡伯仁,森藍,詹醬,706郭芳圻,montana_chen,Jerry,Peter
蔣,蔡芳如,郭宗彥,彭永興
|
|
070526~070601 |
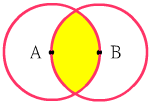 圓A和圓B都是半徑為1的兩等圓,試求右圖中黃色區域的面積? 圓A和圓B都是半徑為1的兩等圓,試求右圖中黃色區域的面積? |
設圓A和圓B相交於C、D點,
黃色區域面積=(扇型ACD + 扇型BCD)-(菱形ABCD)
又因為線段AC=AB=AD,所以角CAD=角CBD=120度
,所以(120/360*π*2)-√3/4*2=(2/3)π-√3/2
解題成功者:wailun wong,蔡伯仁,詹醬,
706薛同亨,montana_chen,Pete蔣,J.J.Lee,
jerry13,阿斌,郭宗彥,天才阿張.
|
|
070514~070525 |
某家書局促銷書籍文具,買100元送40元,滿50元送15元。阿明挑了710元的書,算上優惠的部分,他需要付出510元(滿500送200)就可以了。當賬單打印出來之後,阿明卻發現錢沒帶夠,於是他先付了410元,並留下一本
原價280元的書做抵押,決定第二天將餘款100元補齊後再把那套書取走。到了第二天,阿明卻想退掉抵押的書,而書店也同意退還,試問書店應退給阿明多少元? |
300元可買原價420元的書籍文具
所以只須付310元即
已付給書局410元
所以書局需還給阿明410-310=100元
解題成功者:wailun wong,708阿福 |
|
070428~070514 |
袋子內裝有若干個紅色球和藍色球,從袋子隨機抽出兩個球,若抽出兩個紅色球的機率是抽出兩個藍色球機率的5倍。若抽出一個紅色球和一個藍球的機率是抽出兩個藍色球機率的6倍。試求原來袋子中紅色球和藍色球各有多少個? |
設袋內有紅色球x個,藍色球y個;
則抽出兩個紅色球的機率為:
x/(x+y)×(
x-1)/(x+y-1)
抽出兩個藍色球的機率為:
y/(x+y)×(y-1)/(x+y-1)
抽出一紅球一藍球的機率為:
[x/(x+y)×y/(x+y-1)]×2
依題意列聯立方程式:
x(x-1)= 5y(y-1)
2xy = 6y(y-1)
聯立解出y=3 x=6
即紅色球6個,藍色球3個
解題成功者:蔡伯仁,李昌明,kill3kk,
郭宗彥,Peter蔣
|









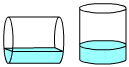

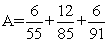 ,
,