|
時期 |
題目 |
解題 |
|
070412~070427 |
一座標準游泳池,水道長 50 公尺,甲乙兩位選手分別在游泳池某一水道的兩端,同時出發相向而游,甲的速度每秒 1 公尺,乙的速度每秒
1.25 公尺,兩人來來回回游了25分鐘,若速度大小不變且不計轉向的時間,兩人共交會幾次。(在游泳池邊相會也要算在內) |
兩人第一次交會需 50÷(1+1.25)=200/9(秒)
第一次交會後再經100÷(1+1.25)=400/9
秒才會再度交會
(25×60-200/9)÷(400/9)=133/4=33.25
故兩人共交會33+1=34 (次)
解題成功者:李昌明,蔡伯仁 |
|
070328~070411 |
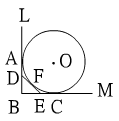 直線L和直線M互相垂直,且相交於B點。若圓O分別和直線L、直線M相切於A、C點,且DE和圓O相切於F點。若直角△DBE的周長是S,試求圓O的直徑? 直線L和直線M互相垂直,且相交於B點。若圓O分別和直線L、直線M相切於A、C點,且DE和圓O相切於F點。若直角△DBE的周長是S,試求圓O的直徑? |
∵AD=DF,EF=EC,∴直角△DBE的周長S=AB+BC=
AO+CO=圓O的直徑。
解題成功者:
曹家駿 ,Winner,小哲,李家瑞 ,Peter蔣,kill3kk,
李沛諺,幻月神翼,玲,蔡伯仁,羅廣群,李昌明,毛毛,李蒼,徐嘉隆 |
|
070316~070327 |
媽媽贏得一筆獎金,並把所有獎金分給家中的所有小孩,她將100元和餘款的十分之一給老大;將200元和餘款的十分之一給老二;將300元和餘款的十分之一給老三,依照這樣的規律將獎金分給其餘的小孩。最後,媽媽發現每一位小孩都拿到相同的獎金,試問家中有幾位小孩子? |
設獎金為x元,依題意
100 + ( x – 100 ) / 10 =
200 + { x - [ 100 + (x-100) / 10 ] – 200 } / 10
得
x = 8100
且
每人得100
+ ( x – 100 ) / 10 = 900元
因此家中小孩有 8100 / 900 = 9
(人)
Ans: 9位小孩子
解題成功者:
YSSY168,陳孟凱,蔡伯仁,李沛諺,李家瑞,Winner,李昌明,毛毛,iself, Peter蔣,幻月神翼
|
|
070307~070315 |
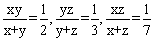 ,求x,y,z的值? ,求x,y,z的值? |
xy/(x+y)=1/2,(x+y)/xy=2,1/x+1/y=2---(1)
yz/(y+z)=1/3,(y+z)/yz=3,
1/y+1/z=3---(2)
xz/(x+z)=1/7,(x+z)/xz=7, 1/x+1/z=7---(3)
(1)+(2)+(3)
2(1/x+1/y+1/z)=12,1/x+1/y+1/z=6----(4)(4)-(1)
1/z=4 ,
z=1/4
(4)-(2)
1/x=3 ,
x=1/3
(4)-(3)
1/y=-1 ,
y=-1
Ans: x = 1/3, y = -1, z = 1/4
解題成功者:
李沛諺,p889013 ,Winner
,法數師,王勝民,銀狐,徐孟弘,溫健淞,森藍,陳孟凱,陳威,林鈺峰,Peter蔣,
幻月神翼 |
|
070224~070306 |
x>0,y>0,x+y=6,試求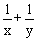 的最小值? 的最小值? |
1/x+1/y=(x+y)/xy=6/xy=6/x*(6-x)=6/[-(x-3)2+9]≧6/9=2/3,所以1/x+1/y的最小值是2/3.
解題成功者:
p889013 ,法數師,王櫻桃 ,chjh08 ,李家瑞,林ㄚ秀 ,森藍,林真,陳孟凱,李沛諺,HsinBokie,婕翎 |
|
07.02.10~07.02.24 |
如圖,圓O內有一正方形ABCD,頂點A和B在圓周,CD邊在直徑上,試求CE︰CD的比值?
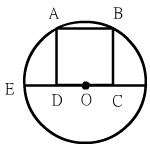
|
令CO=X,則DO=x,CD=2x=CB
連BO
BO=√[(2X)2+X2]=X√5
BO=EO(都是半徑)
EC=EO+OC=X(1+√5)
CE︰CD=X(1+√5)︰2X=(1+√5)/2
解題成功者:
YSSY168,石崑峰 ,p889013 ,李家瑞,吳孝仁,
張沛軒 ,潘宗毅,fish,andy687 ,陳立中,陳先生 |
|
07.01.27~07.02.10 |
一遊行隊伍長達2公里,在遊行中,阿雄以固定速率從遊行隊伍的排尾追到排頭,到了排頭後立即折返。當他回到排尾時隊伍也剛好前進了2公里,如果隊伍的前進速度保持不變,試求阿雄所走的總距離是多少公里?
|
設隊伍行進速率為時速x公里,阿雄的速率為時速y公里(y>x>0),由題意得知
隊伍行進2公里所花費的時間等於阿雄由排尾追到排頭所花的時間和由排頭追到排尾所花的時間之和
因此,得一方程式如下
2/x=2/(y-x)+2/(y+x)
解方程式得
y=(1+√2)x 或者y=(1-√2)x(不合)
所以阿雄所走的總距離是
y×2/x=2(1+√2) 公里
解題成功者:SYSRKL,吳孝仁,潘宗毅,p889013,iget |
07.01.12~07.01.24
|
如果長方形的長=x,寬=y,P點在長方形內或週邊上,試求a2+b2+c2+d2的最小值和最大值?
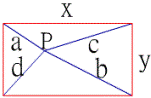
解題成功者:吳孝仁,SYSRKL
|
令 x= r+s,y= p+q
a2+b2+c2+d2=2(p2+q2+r2+s2)
由柯西不等式可知
(p2+q2)(12+12)≧(p+q)2=y2,同理,(r2+s2)(12+12)≧(r+s)2=x2
所以 a2+b2+c2+d2=2(p2+q2+r2+s2)≧x2+y2
另一方面
因為p+q=y,所以p2+q2=p2+(y-p)2=2(p-y/2)2+y2/2
當p=y時,p2+q2有最小值 y2.
同理,r=x時,r2+s2有最小值 x2.
所以a2+b2+c2+d2=2(p2+q2+r2+s2)≦2(x2+y2)
因此a2+b2+c2+d2的最大值是2(x2+y2),最小值是x2+y2.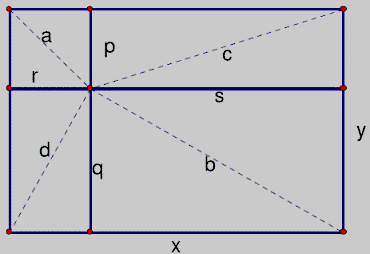 |
07.01.01~07.01.11
|
長方形ABCD,長寬分別是3和2,有一點P在長方形ABCD區域(包括周邊和內部),試計算P點到四個頂點的距離和?
[ 提 示 ]
(1)最短距離和是多少?此時,P點在何處?
(2)最長距離和是多少?此時,P點在何處?
|
(1)如果S點在長方形ABCD內,且S點不是對角線的交點.因為SA+SC>AC且SB+SD>BD,所以SA+SC+SB+SD>AC+BD,因此,P點到四個頂點的最小距離和等於兩對角線和,即2√13,此時P點是對角線的交點。
(2)設S點長方形ABCD內,過S點作直線L//AD交CD於E點,因為SA+SD<AE+ED,且SB+SC<BE+CE.
[參閱提示]所以SA+SD+SB+SC<(AE+BE)+CD<CB+CA+CD.
P在頂點C時,P到四個頂點的距離和最大,其值是5+√13.
解題成功者:溫林悲,HsinBokie,SYSRKL |
|
06.12.26~06.12.31 |
如果a,b,c,d,e,f,都是奇數,試問可否找到一組(a,b,c,d,e,f,)
使得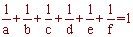 呢? 呢?
如果可以找出來,請寫出你的作法。
如果不能找出來,也請你說明為什麼。
|
等量公理乘以abcdef,得
bcdef+acdef+abdef+abcef+abcdf+abcde=abcdef
.....(1)
因為奇數‧奇數=奇數且偶數個奇數的和是偶數,
依題意知:a,b,c,d,e,f,都是奇數,顯然上列式子(1)不會成立。
解題成功者:peter60803, SYSRKL,
阿真, jean |
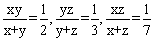 ,求x,y,z的值?
,求x,y,z的值?
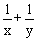 的最小值?
的最小值?


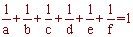 呢?
呢?