 p.2
p.2
 p.2
p.2
����X��X�{�q��j�ǥͪ��DZб¡B���ξǮa�J������]Dr. Gene
Kritsky�^�b�x�����cicadasafari.org���ܡA2024�~��2�ؽ���ͪ��@���۹J�A�e�̤��O�b�a�U�h��13�~�M17�~�~�|�}�g�ӥX�A�o2���ͦP�ɥX�{�n�g��221�~�A�W�@���P�ɥX�{�b1803�~�A���ɪ������`�άO�٬O�ĤT���`�ΡB�}�ꤸ�ԳǦ]Thomas
Jefferson�^�C( 13�M17���̤p�����ƬO221 )
�ͪ����Φb��F����ƫ�|���X�ñ��J�a���p�J�g�̡A�b�a�U�h��h�~��}�g�ӥX�A�o�b��t��X�ѦܴX�P��N�|���h�C�N�b2024�~4�멳�B5���A�_���w�S�����u���|�w13���͡v�]Brood
XIII�^�N�b�h��a�U17�~��}�g�A�|�b��Q�զ{�_���ФơC�P���P�ɡA�u���|�w19���͡v�]Brood XIX�^�]�|�b�h��13�~��}�g�A�X�{�����F�n���a�ϡC
�ѦҸ��: �ͳ��Ͱʪ��� (cicadasafari.org)
�qMental Arithmetic. In Public School of S. A. Rachinsky�r�O�Xù���e�aNikolay Bogdanov-Belsky 1895�~���e�@�A�e�̪��ªO�W�@�D�p���D�J$\dfrac{10^2+11^2+12^2+13^2+14^2}{365}$�C
�]��$10^2+11^2+12^2=13^2+14^2=365$�A�ҥH$\dfrac{10^2+11^2+12^2+13^2+14^2}{365}=2$

13+13+13=3�A43+43+(-5)3=3�C
1953�~�A�ƾǮaLouis
Mordell���X�@�Ӱ��D�G�ux3+y3+z3=3�O�_����3�վ�ƸѦs�b?�v
Charity Engine
�O�@�Ӵ��ѥ��m�a�ιq���K�O�U���@�����q���Ϊ��M�סA2019 �~ 9 ��A��s�H���z�L Charity Engine���X���y40
�h�U�x�a�ιq���B��L�̪��t��k�A�`�@�������X��400�h�U�ӭp����ȡA�����@�x�q���t��3�p�ɪ��B��A�ש���x3+y3+z3=3����3�վ�ƸѡA(569936821221962380720�A-569936821113563493509�A-472715493453327032)�C
(569936821221962380720)3 + ( -569936821113563493509 )3 + (
-472715493453327032 )3 = 3
�����s���Jhttps://www.charityengine.com/
������(Perfect
number)���Ҧ��u�]�ƩM�����ƥ����A�Ҧp�G6=1+2+3�A28=1+2+4+7+14�A�ثe�Ҫ���F�褸2013�~1��25��~�o�{��48�ӧ����ơA�ӥB48�ӳ��O���ơC
�u�@�Ӱ��ƬO�����ơA�Y�B�߭Y���㦳�Φ��G2n-1��(2n-1)�v�A���w�z���R���ʬ��b�褸�e300�~�N�ѼڴX���o�]Euclid�^�ҩ��A�ӥ��n�ʫh��18�@���~�Q�ש�(Euler)���ҩ��A�䤤2n -1�O���(���˽��)�C�̾a�q�����ֳt�B��~��X�Ӫ���48�ӧ����ƬO257885160��(
257885161 -
1 )�A������ƶW�L3400�U���A�e�X��Ʀr�O16929639�A��X��ƬO270130176�C
�u�O�����j��p�Ь��������T�A���a�q�ط�÷�N�]�p�X�ϼˡH�v
�^���֤H�i��
(Alexander Pope) �b�L���@�~�m�H���g§�n�H�o�y�ܦV�Ь������F�q�N�C�Ь����b����1707
�~�o�{�����w�z
(De Moivre's Theorem)�A�褸1722
�~�����o�� (cos�c+i sin �c)n
=
cos(n�c)+i sin(n�c)�A�䤤n�O����ơC����1749�~�ک�
(Euler)�ҩ� n �O��ơA�өw�z�]���ߡC
�����s���G�Ƽƭ��n���X��N�q
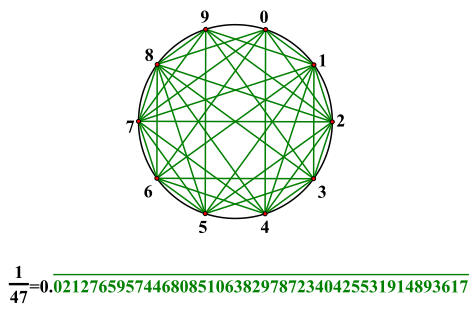

������������εL�k�Q�������A�]������108�X���O360�X���]�ơC�ΦP�@�إ��h��ΨӾQ�������A�s�����^�O�ϡA�u�����T�����^�O�B������^�M��������^�O�A���^�O�ϴN�u���o3�ءC
���O�w��Reinhardt
(�褸1918�~)�o�{�F�D������Ϊ�5�ؤ�����^�O�A���ܦ褸2012�~�ƾǮa�̧��14�ؤ�����^�O�C�褸2015�~�A����ز��y�j�Ǩ������(University
of Washington, Bothell)���T��ƾǮa Casey
Mann�B Jennifer McLoud�B�M David Von Derau�H�p����t��k����15�ؤ�����^�O(��1)�A�o�Ӥ���Ϊ��������O�O60�X�B135�X�B105�X�B90�X�B150�X�A��������O
1�G1�G2�G1�G(��2+��6)/ 2�C
Casey
Mann�B Jennifer McLoud�B�M David Von Derau�H�p����t��k����15�ؤ�����^�O(��1)�A�o�Ӥ���Ϊ��������O�O60�X�B135�X�B105�X�B90�X�B150�X�A��������O
1�G1�G2�G1�G(��2+��6)/ 2�C
�ѦҸ��:
(�� 1)�G15�ؤ�����^�r�Ϯפަ�
https://commons.wikimedia.org/wiki/File:PentagonTilings15.svg
�����p����Ǫ� Japp Van den Herik�BUiterwijk�BVan
Rijswijck���H�b�褸2002�~�A���u�����C���v�U�F�w�q�G�Y�ӹC���O���⪺�C���A�B���a����ǿ������v�O�۵����A�N�i�H�٦��C���O�������C�p�j�a�Ҽ��x���r��e�C���M���l�ѳ��O�����C���C
Awari
�C���O�y�ǩ�D�w3500�~���j�ѹC���A�ƦܬO�{������ѡA�@�����褸2002�~�A���Щ��������i���S�����ۥѤj�Ǫ��G��p����H�u���z�Ǫ�John
W. Romein �M Henri E. Bal�P�ɧQ��144�ӭp����B�z���@����p���A�Ӯ�51�p�ɡA�}��Awari
�C���� 889‚063‚398‚406�Ӥ��P�����k�A�ҩ����O �����C���C
�����C���C
���ǤH�U���w�˦b����M���O�q�����_�۴ѹC���N�OAwari
�C���C
�����s��:
�_�۴ѹC��(swf���A�ثe�u��b�q������)
�[���j�HPhilippe Chrétien�ھڵ�i�ԫ��ƦC���e5��1,1,2,3,5�ۥ[�M����12�A�]�p�X�@��12�p�ɨ��i�ԫ������C�b�������譱�W����5�ӥ���ΡA�Ѥp�Ӥj��������O�O1�B1�B2�B3�B5�A�ӨC�@�ӥ���Ωҹ������Ʀr���O�O1�B1�B2�B3�B5�A�ðt�X���B�šB��B��4���C�⪺LED�O���A�G���O�M�G�ſO������Ωҹ������Ʀr�M���ܤp�ɡA�ӫG��O�M�G�ſO������Ωҹ������Ʀr�M��5���ƪ��ܤ����A�G�տO������Ϋh����ơC�Ҧp
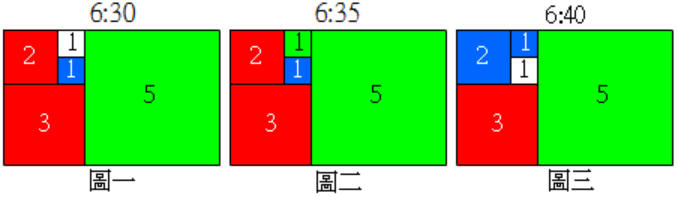
�Ϥ@�G(2+3+1)�p�ɡA[(5+1)��5]��
�ϤG�G(2+3+1)�p�ɡA[(5+1+1)��5]��
�ϤT�G(3+2+1)�p�ɡA[(5+2+1)��5]��
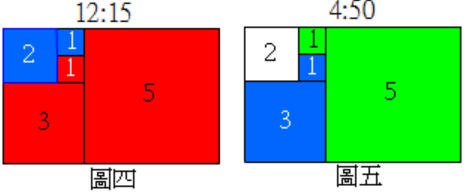
�ϥ|�G(5+3+1+2+1)�p�ɡA[(2+1)��5]��
�Ϥ��G(3+1)�p�ɡA[(5+1+1+3)��5]��

2010�~�O�����¬ٲz�u�ǰ|(MIT)�خ�150�P�~�A���@��ΦW�H�h���U�@�y�W���uAlchemist
�v���H���J��æbStratton �ǥͤ��߫e�s���i�ܡA�uAlchemist �v���@�̬O��Z���ڶ붩�Ǫ����N�aJaume
Plensa�A�L�ϥΤ��ÿ������ơA�ĤJ�F150�ӼƾDzŸ��@���Ч@�����A��y�F�@�y�P���u�a�ӧ����H���J��C
�Ϥ��ӷ�:
http://listart.mit.edu/public-art-map/alchemist
 �֧J���ʵe�u�@��(Pixar)�H�z���G�ƩM�s�@�ʵe�D�W�A�L�̩ҥX�~���m�����`�ʭ��n�B�m�W�H�S�n�B�m�Ʋz�����n�B�m�ˤO�n�B�m�ѥ~�_�ݡn�B�m�����`�ʭ�3�n�Ρm�i���ǻ��n����o�����d���Ϊ��y�����a�C���O�A���H���ƻ�ϱo�J�}�M��L�A�߷R���ʵe�H���A���F���{���e�{�b�A�ڲ��e�A���N�O���æb�ʵe�I�᪺�ƾǡA�]�t��N�B�T����ƩM�X��ǡB�u�ʥN�ơB�L�n�����C�Ҧp�G�m�����`�ʭ��n�̪��J�}�����ʩM����N�O�B�Χ��Х����X�����M�T����ơC�m�i���ǻ��n�̪��u�����F�v�Ҭ諸��A�P�y���B����N�O�B�βӤ�(subdivision)���������u�ơA�Ӥ���X�F���u�q���I�B�������ΡB�����u���A�гy�F�ʵe�����⪺3D�~���C
�֧J���ʵe�u�@��(Pixar)�H�z���G�ƩM�s�@�ʵe�D�W�A�L�̩ҥX�~���m�����`�ʭ��n�B�m�W�H�S�n�B�m�Ʋz�����n�B�m�ˤO�n�B�m�ѥ~�_�ݡn�B�m�����`�ʭ�3�n�Ρm�i���ǻ��n����o�����d���Ϊ��y�����a�C���O�A���H���ƻ�ϱo�J�}�M��L�A�߷R���ʵe�H���A���F���{���e�{�b�A�ڲ��e�A���N�O���æb�ʵe�I�᪺�ƾǡA�]�t��N�B�T����ƩM�X��ǡB�u�ʥN�ơB�L�n�����C�Ҧp�G�m�����`�ʭ��n�̪��J�}�����ʩM����N�O�B�Χ��Х����X�����M�T����ơC�m�i���ǻ��n�̪��u�����F�v�Ҭ諸��A�P�y���B����N�O�B�βӤ�(subdivision)���������u�ơA�Ӥ���X�F���u�q���I�B�������ΡB�����u���A�гy�F�ʵe�����⪺3D�~���C
�����\Ū�G
The math behind the movies: An interview with Tony DeRose of Pixar
2013�~11��1��A���f�L���m�ݨ��x�W�n�������H�ũ秧�ﳾ���������A�N�x�W�H�@�اA�q�����L�����P���A�A�e�{�b�j�ȹ��W�C�P�ɱa�_�@�Ѫũ窺����A���|�b���澹�������P���~�A�i�O�A���D�|�b���澹�p��֦��F���B�ʤO�ܡH ���A�o���o�U��ƾǺt��k........
���A�o���o�U��ƾǺt��k........
�u�μƾǼҫ����������欰�����z�k�h �A�M��μƾǪ��@�Ӥ���--"����z��"�Ӥ��R�o�Ǽҫ��æX������t��k �C�Ҧp�ڭ̷Q���|�b��a�a���A�ڭ̭����Τ@�շL����{���Ӯ����ʺA �A�M����a�o�ǷL����{���A�ño�U��z�إߪ��t��k���|�b�o�Hí�w �v�C
�H�U�Ӧ�TED���v���N�X�j�ƾǪ��Ѫ�����
�Ե�ù�w�w�P (Raffaello D'Andrea): �|�b���澹��H���B�ʯ�O
�s���I�P�I�A�غc�X��ϧΤ��O�����A���O�n�b��q���u�ϤW�e�{�ʪ��Ϲ��A�o�ݭn�зN����C
1988�~�^�����N�aPaul Middlewick �����N�۴��a�K���y�D�B���I�B����I�s�����@���j�H�A����S����Ч@�F35�i�ʪ��Ϲ��C
�����s��: �b�^��۴��a�K���ʪ�
�ƾDz��~�A��߮��ءA�N�s���@��|��A���ζ��@��|��æb��I����W���J�O�C��I���O���@���u�A���U�ϥѥ��ӥk���O�O��ΡB���B�ߪ��u�B�����u�C


�ϧΤަ�
www.evilmadscientist.com/2013/sconic-sections/
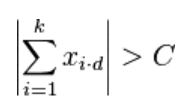 �H�����Y�ɪO�A�����¤W�O��+1�A�ϭ��¤W�O��-1�A�p�G���Y�D�`�h���A�ðO���C�@�������G�Φ��@�ӼƦC�C
�H�����Y�ɪO�A�����¤W�O��+1�A�ϭ��¤W�O��-1�A�p�G���Y�D�`�h���A�ðO���C�@�������G�Φ��@�ӼƦC�C
�I���Q�ƾǮa�Où.��f�E(Paul Erdos)�b�褸1932�~���X�uthe Erdos Discrepancy Problem�v���q�Q�A�L�{���i�H�b��+1�P-1�ҧΦ����L�a�ƦC�A���@�Ӧ������l�ƦC�A�Ӥl�ƦC���U���`�M�j��w�����`��C�C �褸2014�~2��A�^���Q�����j�Ǫ��p����M�aAlexei Lisitsa�դh�MBoris Konev�դh�Q�ιq�l�p���(�q��)�ҩ��F��+1�P-1�H���զ��B����1161���ƦC���w�s�b�@�Ӥl�ƦC�A�Ӥl�ƦC���U���`�M�j��2�C�q���g�L�j��6�p�ɪ��p��A�]�t�ҩ��Ӹ`���ɮפj�p�j���O13Gb�A��_���W������ʬ�������e�q(�j��10Gb)�٦h�A�H�P�D�`���ΤH�u�������ǽT�ʡC�o�N�l�ͥX���D�G�u�q���ҩ��ƾǩR�D�A���O��ƶq�L���e�j�A�H�ܩ�L�k�ѤH�u�i�����ҡA����o���ҩ��O�_��O���T�O�H�v�i�O�b�{��̡A�q�������ƾǬ�s���u��w�O�j�թ��͡A�ݭn���j�B��q���ƾǰ��D�A�j�h�Ʊ��p�]�u��a�q���������A�q�����b�X�i�ƾǬ�s����k�A�é����ƾǬ�s���då�C�L�h�A�|����D�BE8���c�BFekete���D�BKepler
�q�Q���ۦW�ƾ����D�A���O�ɧU�q�����ҩ����C

Google�b2013�~11��4�骺���������]Google Doodle�^�O�L�ƾǮa�L�b��ԡE�����]Shakuntala
Devi�^�M�p������ϼˡC
�L�b��Ԥ��~(2013�~)4��21��]�I�l�D�M��Ŧ�e�f�L�@�A�ɹ�83���C�u�ì��ɳ��v�ήe�o�O�ߺ��O��H���ƾ��]�k�v�A1977�~�A�o�b����w�{�F�Դ��]Dallas�^���n�òz���|�j��
9167486769200391580986609275853801624831
0668014430862240712651642793465704086709
6593279205767480806790022783016354924852
3803357453169351119035965775473400756816
8830562082101612913284556480578015880677
1��23����ڡA�ӷ��ɳQ�Ψ���⪺�q��Univac1108�h��F62������F��13000�D�{�Ǥ~��X���סC
�غ��������媩2013/10/15�Z�n�@�g����<���ƹ�Ǧn�ƾǦ��h���n�H>����G�u���껫�{�d��������j��(Carnegie Mellon
University)�{���߲z�DZб��j�k�O�Ʈ��(Bob
Siegler)2012�~��Ϊ��@����s�o�{�A�ǥͤ��~�Ůɴx�������ƪ��ѯ���w���䰪���ƾǽҪ����{�A�b�ư����ӡB�\Ū���Z�B�u�@�O�ФO�B�a�x���J�M�Ш|�B��ƪ��ѵ��]�����v�T��]�O�p���C�v

�W�C���`���p�Ƴ��O1/3������A��6�Ӽ�1/729���`���`�ܪ��A�`���`�t��81�ӼơC�ը������z���o�D�O���]Richard
Feynman�^�W���5�Ӽ�1/243������A�����`���`�O 004 115 226 337 448 559 670 781 893�A�䤤
115-004=226-115=337-226=448-337=559-448=670-559=781-670=781-670=111�A893-781=112�C
�W�@�a����ÿ���m���B�n��G�̪�<�V���n>�B<�O�H���v����>���ΥL�b�x�n���\�j�ǫȮy���Ҵ����M�p�ǥʹ��Q�׳o�өǼ�1/243���G�ơC
�����\Ū:
�褸
1966�~�A���a�Q�ƾǮa Leo Moser ���X�@�Ӱ��D�G�u�����W�A�p�G���@�D�ਤ�O90�ת����Y, ���Y�e 1 ���ءA�p�U���ϡA�h�@�ӥi�H�����q�L�������s���F�o���n����H�v
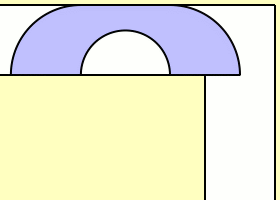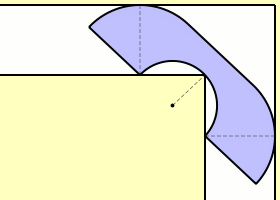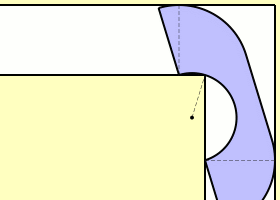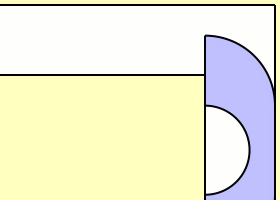
(�Ϲ��Ӧ�:Wikimedia
Commons)
�����\Ū:
www.math.ucdavis.edu/~suh/gerver-moving_sofa.pdf
�W�Ϥ�����y��O�}��i���e����L�b�a���d�U������A�A��P�_�o���}�O�V�k��i�٬O�V���ܡS
�e���d�U���y��O���Ⲫ����ŦⲪ��O�S�o�Ӱ��D���g�X�{�b�褸1903�~�ֺ����������p���mTheAdventure of the Priory School�n
(Arthur Conan Doyle�ۧ@)
�ѦҸ�ơG
Bicycle tracks
Mathematical Impressions- Bicycle Tracks
Bicycle Diagram (mp4�v����)
���w���ɡm�֦~Pi���_�ۺ}�y�n�a���85�������d�������̨ξɺt�A�m�֦~Pi���_�ۺ}�y�n�]Life of Pi�^�O�@�մy�z�@�W�L���k�ġuPi�v�b�ӥ��v�W�P���~�s�[�Ԫ�z��E���J�]Richard Parker�^�P��Ӽ��L227�Ѫ��ͦs�G�ơC22/7�O��P�v�k������ȡA�褸�e250�~����̱o�p��X��P�v�k����223/71 �M 22/7�����C
�褸2013�~�A2013=3��11��61�A2013�O�T�Ӭ۲���ƪ��s���n�C���X���O���U�ӤG�~���褸��2014�B2015�]���O�T�Ӭ۲���ƪ��s���n�A2014=2��19��53�A2015=5��13��31�C�շQ�@�Q�T�ӳs���Ƴ��O�T�Ӭ۲���ƪ��s���n�A�٦����ǩO�S
�@�ӥ���ƥi�H�g���@�ǥ���ƪ��M�C�b�ƽפW�A��o�ǩM�����������D�٧@��Ƥ���(integer partition)�C
�Ҧp:
2=1+1�A��2�ؤ��Τ覡�A�ҥHp(2)=2�F
3=1+2=1+1+1�A��3�ؤ��Τ覡�A�ҥHp(3)=3�F
4=3+1=2+2=2+1+1=1+1+1+1�A��5�ؤ��Τ覡�A�ҥHp(4)=5�C
���~�A
p(8)=22
p(16)=231
p(32)=8349
p(64)=1741630
p(128)=4351078600
p(256)=365749566870782
p(512)=4453575699570940947378
p(1024)=61847822068260244309086870983975
2011�~1��21������J�q�z�j���]Emory
University�^���ƾDZб�Ken Ono�M��s�ζ��N�o����s�ƽס���Ƥ��Ρ�(integer
partition)���s��k�A�L�̵o�{��Ƥ��Ϊ��ǦC���c�N���O����(�H�ΡAfractal)�A�ùB�ΥL�̩ҵo�{�����(Ken
Ono�٦���Ƭ�P)�i�H�H�������B�N�ƪ�����(�p�U)�p��X�Ҧ���ƪ����μƥءC

(�K����Ono��²���v��)²���v��(youtube)/��������/ ²���v��
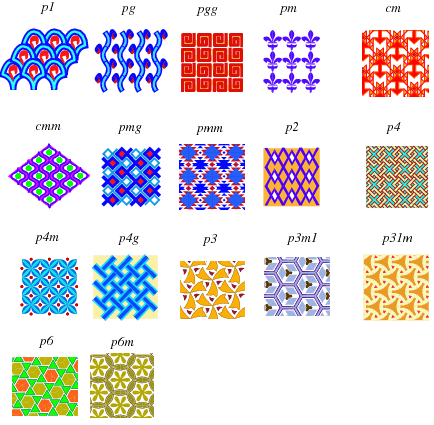
�u�������������Ϯץi�H���@�p�������᯾�z�L����B½��B��g�B�������覡�A��ӥ����O�H�v�ƾǮa�w�g�ҩ����� 17
�������A�o�إ�����٫��A�Q�٬��uWallpaper group�v�A�p�U�ϡC
�Ϥ��ӷ�:
http://mathworld.wolfram.com/WallpaperGroups.html
�����\Ū:
http://xahlee.org/Wallpaper_dir/c5_17WallpaperGroups.html
java�i�ܵ{��:
Download Escher Web Sketch
�~�פF�A�N�e��2011���2012�A�����ù���F�{(Florida)�v���ˤj��(Stetson University )�ƾǨt�Ʊб� Erich Friedman �]�p�F�@�y�Ʀr�g�c�A�J�f�B�O2011�A�i�J��i�H���B�䶡�A�J��⦡�N�B��A�A�i�H���ƨ��L�����A���O���i�H���^���訫�L�����A�p�G�b�X�f���B��G�O2012�A�N�O�L���F�C
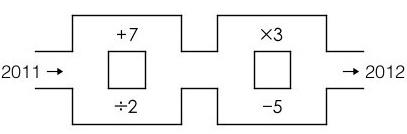
�Ѧҵ���:
(((((((((((((((((((((((((((2011 +7)
��2) +7) ��2) +7) -5) ��3) ��2) +7 )��2) +7) ��3) -5) ��2) +7) ��2)
+7) -5) ��3) -5) ��3) ��2) +7) -5) ��3) ��2) +7) -5 = 2012
�ѦҺ���:
www2.stetson.edu/~efriedma/holiday/2011/index.htm
 19�@���k��ƾǮa�ť߸�(J.
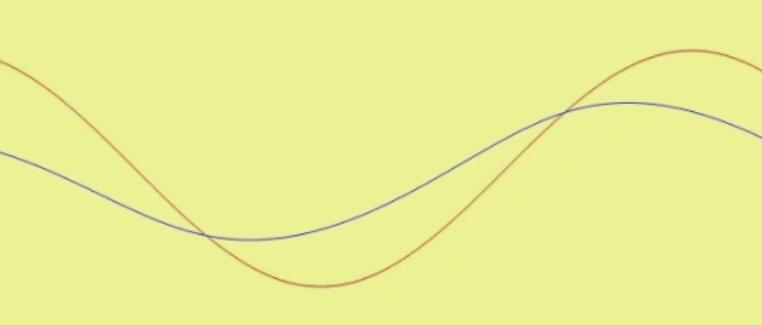
B. Fourier, 1768-1830)
�A�ҩ��F�Ҧ������n�A�]�A���֩M�n�ֳ��O�@��²�檺�����P����ƪ��M�C�ť߸����o�{�A�ϤH�̥i�H�N�n�������աB���q�B����z�L�ϸѨӥ[�H�y�z�M�ϧO�C���ջP���u���W�v�����A���q�P���u�����T�����A�ӭ���h�P�P�����Ϊ������C
19�@���k��ƾǮa�ť߸�(J.
B. Fourier, 1768-1830)
�A�ҩ��F�Ҧ������n�A�]�A���֩M�n�ֳ��O�@��²�檺�����P����ƪ��M�C�ť߸����o�{�A�ϤH�̥i�H�N�n�������աB���q�B����z�L�ϸѨӥ[�H�y�z�M�ϧO�C���ջP���u���W�v�����A���q�P���u�����T�����A�ӭ���h�P�P�����Ϊ������C
�ѦҺ���:
www.phy.ntnu.edu.tw/java/sound/
�^��m�s��Ǯa�n����2010/8/11��Z���@�g����ƾǮa�i��ѨM�F�p���������DP��NP���峹�A����f�������(Hewlett-Packard
Labs)���ƾǮaVinay Deolalikar�w�g��2010/8/6�鴣��F�ҩ�P��NP���פ��Z�A�p�G���פ�Q�f�ֵL�~�A�h���ܤC�j�@�ɼƾ����D���@��P���D(�h������k)��NP���D(�D�h������k)�ש״���C�åi��o�Ѭ���J�p�ƾǬ�s�Ҵ��Ѫ�100�U���������C
�ѦҸ�ơG
NewScientist
2010�~7��A�]�A Morley Davidson�BJohn
Dethridge�BHerbert Kociemba and Tomas
Rokicki ���H����s�ζ��ҩ����N�զX���T���]�N����i�H�b 20
�B���٭�C�{�b�W�Ҥ��ƥ����w�� 20 �C
�ѦҸ�ơG���]�N����i�H�b 20 �B���٭�C�{�b�W�Ҥ��ƥ����w�� 20
�C
�ѦҸ�ơGGod's
Number is 20
�۵M�ɪ��ƾ�...
 ��Nikon(���d)�٧U�|�쪺2010�~��L�Ӥ����ɴ���A10��13��������a�a�z�������ɱo���Ӥ��A�A�l����Ŧ��o�����C�k�ϬO����Ӥ����@�A�M���i�����p���Ʋ��Ѳ��h������Τp����K�զX�Ӧ��C
��Nikon(���d)�٧U�|�쪺2010�~��L�Ӥ����ɴ���A10��13��������a�a�z�������ɱo���Ӥ��A�A�l����Ŧ��o�����C�k�ϬO����Ӥ����@�A�M���i�����p���Ʋ��Ѳ��h������Τp����K�զX�Ӧ��C
�ѦҺ���:
�����a�a�z����
�`�Ǻ��E�p���դh���A�e�����F�Ļe�A�b���_�M�ᦷ�������ӭ��h�A�o�O�@��ܯӺ�O���Ʊ��A�]����ڤW�e�����b�ѨM���Ȧ�Ӱ��D��(Traveling
Saleman Problem�ATSP)�C�o�O�����o�{��ѨM�o�Ӱ��D���ʪ��A��s���i�Y�N�o���b�m����ժ��Ǯa�n���x�C�p�G��z�ѻe����˰���o�@�I�A��H�����Ͳ��B�ͬ��N���ܤj���U�C
 �Ȧ�Ӱ��D(Traveling
Saleman
Problem�ATSP)�S�٬��Ȧ���P�����D�A²�٬�TSP���D�A�Ӱ��D�O�b�M�D��@�Ȧ�̥Ѱ_�I�X�o�A�q�L�Ҧ����w�I����A�̫�A�^����I���̤p���|�M�C�̦����Ȧ�Ӱ��D���ƾdzW���O��Dantzig�]1959�^���H���X�A�ثe�����W�Źq������U�B��A���S���̨ε��G�C(2010/10/31)
�Ȧ�Ӱ��D(Traveling
Saleman
Problem�ATSP)�S�٬��Ȧ���P�����D�A²�٬�TSP���D�A�Ӱ��D�O�b�M�D��@�Ȧ�̥Ѱ_�I�X�o�A�q�L�Ҧ����w�I����A�̫�A�^����I���̤p���|�M�C�̦����Ȧ�Ӱ��D���ƾdzW���O��Dantzig�]1959�^���H���X�A�ثe�����W�Źq������U�B��A���S���̨ε��G�C(2010/10/31)
�����\Ū:
�Ȧ�~�ȭ����D

2010�~12��A�q�v�|�u�W�M�uAgora�v�Aagora��N�O��þ�����������A�Ӱꤺ�N�v���R�W<���ɨΤH>�A�Ѵ��������d�̨Τk�t�����^���k�P����h��(Rachel
Weisz)�D�t�C����h���ҧ�t�����⥿�O�ƾǮa���ڮL
(Hypatia�A370��415 AD)�C
�ĥ|�B���@���A�Fù���ɥN�����A�b�_�D�J�ΨȾ��s�j��
(Alexandria) �����ڮL
(Hypatia) �O�H���v�W���Ĥ@��ǥX�k�ƾǮa�B�Ѥ�Ǯa�M���Ǯa�A���ڮL�~�������B�G�~�B�~�w�ƨ��ɤH���g�C�o�C�ǹL����A�b�վǰ|�̱б¼ƾǡB�Ѥ�ǩM�s�f �Թϭ���
(Neoplatonic philosophy)�C�b�ƾǩM�Ѥ�譱�A�o���¨õ���²�����ɳ̲`�����ǰݡAĴ�p
Apollonius ���m�G���@�u�סn(Treatise on Conic Sections)�A�N�ƻ�
Diophantus ���m�N�ƾǡn(Arithematica)�A�Ѥ�B�ƾǩM�a�z�v�� Ptolemy
���W�ۡm�Ѥ�Ǥj���n�μڴX���o���m�X��쥻�n���C
�Թϭ���
(Neoplatonic philosophy)�C�b�ƾǩM�Ѥ�譱�A�o���¨õ���²�����ɳ̲`�����ǰݡAĴ�p
Apollonius ���m�G���@�u�סn(Treatise on Conic Sections)�A�N�ƻ�
Diophantus ���m�N�ƾǡn(Arithematica)�A�Ѥ�B�ƾǩM�a�z�v�� Ptolemy
���W�ۡm�Ѥ�Ǥj���n�μڴX���o���m�X��쥻�n���C
�W�ϬO�q�v�uAgora�v<���ɨΤH>�@�ӡC�k���A�����_���ɴ��q�j�Q�W�e�a�Դ����b�e�@�m����ǰ|�n����ø���զ�k�l�A��@�w�H�N�O���ڮL
(Hypatia)�C
�����\Ū:episte.math.ntu.edu.tw/articles/mm/mm_16_4_13/
�饻�@�P��( Kyodo News Agency)2011�~10��17����ɡA Shigeru Kondo (���íZ)�ť��w�g���\�ϥΦۤv�ո˪��q������t��k���{���A�p���P�v��p���I���10����]1012)�A�ӥB��10����Ʀr�O5�C�W�V�F�ۤv�b2010�~8�뤽�����p���I���5����A�өһݭn���w�Юe�q�]��2010�~��22TB�j�W��48TB�A����{��(�����s��-�Ⱦ��s�j�]�p)�p�⪺�ɶ��N��@�~���ɶ��A��W�������h����F��9�Ӥ몺�ɶ��C(1TB=1024GB)
 2010�~8��2��A�饻
Alexander J. Yee
(�E����)�AShigeru
Kondo
(���íZ)�ť����\�Q�ιq���]�{���t��X��P�v��p���I����5,000,000,000,000���
(5��1012)
�CAlexander
J. Yee(�E����)�ҳ]�p���t��n��D�n�O���ΤFv0.5.4.9138
y-cruncher�����k���p��{���A�æbShigeru
Kondo(���íZ)���q���W�����_����F90�Ѫ��B��C���Ҥu�@�h�O�b��x�q���W�������A�o�حp�⪺�W�ҡA�ݭn�Ψ�j�q���O����M22
TB ���w�СA�åB�ݭn3.8 TB ���w�Ш��x�s�w�g���Y�F���Q�i��M�Q���i�쪺�B��ƾڡC
2010�~8��2��A�饻
Alexander J. Yee
(�E����)�AShigeru
Kondo
(���íZ)�ť����\�Q�ιq���]�{���t��X��P�v��p���I����5,000,000,000,000���
(5��1012)
�CAlexander
J. Yee(�E����)�ҳ]�p���t��n��D�n�O���ΤFv0.5.4.9138
y-cruncher�����k���p��{���A�æbShigeru
Kondo(���íZ)���q���W�����_����F90�Ѫ��B��C���Ҥu�@�h�O�b��x�q���W�������A�o�حp�⪺�W�ҡA�ݭn�Ψ�j�q���O����M22
TB ���w�СA�åB�ݭn3.8 TB ���w�Ш��x�s�w�g���Y�F���Q�i��M�Q���i�쪺�B��ƾڡC
(��:��P�v�O���`���L���p�ƪ��L�z��)
�ѦҺ���:
www.numberworld.org/misc_runs/pi-5t/announce_en.html

2010�@�ɨ��y�ɥ��b�n�D�|��A�N�����OZakumi�A��Ķ�W�s�u��w�̡v�C�L�O�@����v�H�ΰ\�A�b2008�~9��22��V�����o���C�L���W�r�uZA�v�����n�D��ISO
3166-1�N�X�A�ӡukumi�v�h�O�U�ثD�w�y����10
���N��C
[��]�x�W��3166-2�N�X�OTW�C
�ѦҺ���:
2010�@�ɨ��y�ɩx�����
Gömböc���褣�˯άO2010�~�W���@�ɳ����|�I���Q�]�Үi�ܪ��@�~���@�A���O���ƾǮaGábor
Domokos�]�I���Q/���F�ش��N�ǰ|�^�M
Péter Várkonyi
�]����/���L���y�j�ǡ^�Ҧ@�P�гy�A�����P��ڭ̩һ{�ѩ����n�j�B�������q���������˯��AGömböc�o�O������a���ê��A�ثe�I���Q�]�����������x�D����W���C
��������:
2010�@�շ|�I���Q�]

�^��º��S���X�{�@�ӳ��а�A�Ϯ���ܥH2�i��g�X�کԩw�zei(pi)+1=0�A�o�Ӧ��l�O�ƾǮa�����̬��R�������C��
e���G�i��ascii�X�O01100101�A^(幂��)���G�i��ascii�X�O01011110�Ai���G�i��ascii�X�O01101001�A�Ϯפ��Hhi���Npi�A���ӥu�O�������|�C

 �饻�ƾǮa����p�N(Kokichi
Sugihara)���]�p"���i��ij������(impossible-motion)"�̪���o�F���꯫�g�������ʬ�s��(The
Neural Correlate Society)�b�����ù���F�{�|�쪺2010�~�׳̨ο�ı���ɪ��Ĥ@�W�j���C
�饻�ƾǮa����p�N(Kokichi
Sugihara)���]�p"���i��ij������(impossible-motion)"�̪���o�F���꯫�g�������ʬ�s��(The
Neural Correlate Society)�b�����ù���F�{�|�쪺2010�~�׳̨ο�ı���ɪ��Ĥ@�W�j���C
�\�h�H�������L�k�T�w������Ŷ��O�_�����ө�����g���A�^��۴��j�ǬӮa�N�����ǰ|(University
of London's Royal Holloway College)�ƾDZб¥��ܧJ��( Blackburn)���t�X�H�U����![]() = (�ۥΨ��������~�A�һݭn�������Ŷ����̤p��)�C
= (�ۥΨ��������~�A�һݭn�������Ŷ����̤p��)�C
�����A�r�p���ݭn���D�ۤv�R�������s�b�|(R)�H�Ϋe����Z��(L)�C�M��A�ٻݭn����X�q���e�������I�쨮�l�̫e�ݪ��Z��(K)�A�̫�A�r�p���ٻݭn���D���b�ۤv�����䪺���l���e��(W)�C���ܧJ�����A�o�Ӥ����o�X���Ʀr�A�O���F�ۨ������~�A�ٻݭn�������Ŷ��̤p�ȡC
��ƨӷ�:
www.telegraph.co.uk/motoring/news/6784428/Scientists-create-formula-for-perfect-parking.html
�C��l����2009�~12��16����ɤ@�h�s�D�AJim�M�L���ζ��ѦҼƾ�Apollonian gasket(�p�k��)�b���ꤺ�عF�{�©��F�z(Black Rock
Desert in
Nevada)�A�s�@�X�@�ɤW���n�̤j����T�����F�a�e�@�A�P���W�L�Q�|�����A�F�e���|���������A�j��餺���j���@�d�h�Ӷ�A�`���n��90���褽��,�۷���ì��ҫ��y�A�Y�Ϧb�@�U�G�d�h���ت����Ť]�ݱo��C
�L�̧Q��GPS�ìP�w��t�γ]�w���СA�Ө��o���T�����סA�M��Υd������ĺ��b�F�a�W���Ы����A������骺�u���̼e�i�F8.5���ءA���Ǧa�誺�`�ױN��@���ءC
�ѦҺ���
www.dailymail.co.uk/news/article-1236380/Worlds-largest-artwork-etched-desert-sand.html
en.wikipedia.org/wiki/Apollonian_gasket
����(�d�J)�쾹�ѹ`�v�X���s������W��(�W��=���ꪽ�|=39�@��)�A
�{�s���k��
�ھ����Ϫ���ڭp�q��(BIPM)���A��ӫo�o�{��F50�L�J�C

 �Ӷ��]�|�g�Ʀr
�Ӷ��]�|�g�Ʀr
�Ϥ��A���ǫG�I�զ���8 �r�Φ��u�A�N�O�ҿת�"����"(Analemma)�C�Ӧ��u�O�b�a�y�W�@�~���C�@�Ѫ��P�@�ɶ��b�P�@�a�I�ҩ��᪺�Ӷ��y��C
�ѦҺ���:
http://antwrp.gsfc.nasa.gov/apod/ap071002.html
http://antwrp.gsfc.nasa.gov/apod/ap071204.html
�ƾǹC��: (�s���C������)
�D�w�ѡ]Mancala�^�A�O�@�ب�H��������C���A�C���L�����_�h���Ѥl�v�@�x�i�Ѩ㪺�U�p�}���A�C���y���D�w��a�H�ΨȬw���F�a�ϡC�]���y��ϰ줣�P�A�o�C���]�l�ͥX�h�اΦ��A�M�{�N�ơB�ӫ~�ƪ��~�ءC�䤤Kalah�����k�O
�u��v��@�p�}�ç���}���Ҧ��Ѥl�A�f������V�v�@���t�@���Ѥl��U�p�}�A�ݭn�g�L�v�誺�p���}�C�Y�̫���t���@���Ѥl���b�v��p���}�ɡA�Ӫ��a���ݿ�ܥ��@�v��p�}�A�A�i����t�ʧ@�C�Y�̫���t���@���Ѥl���b�v��쥻�L�Ѥl���p�}�̮ɡA�ӹ��۹諸�p�}�٦��Ѥl�ɡA�i�N���t���̫�@���Ѥl�P���۹�p�}���Ѥl�����o�C�v
��
�� �n �� /
�¥մ�(½���)
 ½��Ѭ������
½��Ѭ������
�@�ɤW�̶ꪺ����
�w�����۷�J��߫q�žǬ�s�Ҫ���s�����A�L�̱N�Q�Τ@�Ӫ��|10���̪����y��A
�ӫإߤ@�Ӥ��ھ���W��|�X��ǽT���зǴ��q����A�L�̱N�b2011�~�N�o�Ӳy��浹
��ګq�ũe���|(International Committee of Weights and
Measures)�Q�רϥΡA��
�o�Ӫ��|10���̪����y��]�N�����@�ɤW�̶ꪺ����C

�}�ѭ^����а�K�X(2008/6/29)
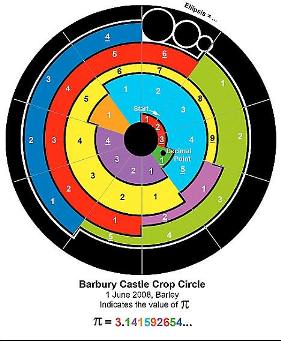
2008/6/18�^���C��l���������w�б�(Mike Reed)�}�ѤF�����~�X�{�b�j�B�z���� (Barbury Castle} ���@�ӳ��а�A�p�G�N���t�b�ϧΪ��T���٭�A�o�{��O��P�v���e�Q�ӼƦr�C���w�б�(Mike Reed)�������A�]�����а�~�Q�ӵ������L�O�A�t�ܶ�P���Ӥ����Q�����F�H���߶�������A�e�X��������P�Q�����u��A�åΤ��P�b�|�������A�N�i�٭��ӱK�X�C�L�N�̤�����������X�o�I�A���η�������A�C�Ӷ���N���@��ơA�Ӷ��誺��ƴN�O�o��Ʀr���j�p�C�Ҧp�A�Ĥ@�Ӯ��ιL�T���Q�����u�A�]���O�u3�v�F���ۡA���ΦV�~���ʤ@��A�N���O�U�@��ơF�Ӯ��ή��䪺�@�I�A�h�N���p���I�C�L�Q�ιq��ø�ϥX�F�@�ӸԲӪ���P�v�ѪR���A�N��P�v���e10�ӼƦ���Ӥ��P���b�|�A�Τ��P�C��M���P��ƪ�����ӥN���F3.141592654���Ĥ@�ӼƦ�3�A�b�̾a���߳B��3��������ӥN���A�p���I�Τ@�Ӷ¶��I�N���A1�h�Τ@�������N���A4��4�浵�����N���A4�᭱��1�Τ@��������N���A1�᭱��5��5���Ŧ����N���K�K���U�Ӫ��C�ӼƦ쳣�Τ��P�C�⪺����N���A�åB�C�ӼƦ�Ҧb����Υb�|�A���n��e���@�ӼƦ�j�@��C�b�̫�@�ӼƦ�4�᭱�A�h�O3�Ӷ¦⪺���A���ܧR�`���H�x��P�v���L�a�L��(���`�����L���p��)�C(������ۭ^��C��l��)

�Υ˯�-�J�������Ҥ�{��
�^ ��۴��Ӯa�j�����μƾǨt(
Applied MathematicsImperial College London)�F��-�J�ҭ}(Darren
Crowdy)�б¦b�O�άM�g�dzN�����o�F��}�ʶi�i�A�Ϩ�i�Q���Ω��������Ϊ��C�æb�̷s�@��(March-June 2007)�X�����m�C�����ǾǷ|�ƾǶi�i�n(
issue of Mathematical Proceedings of the Cambridge Philosophical
Society)���x�W�o���L��Υ˯�-�J�������Ҥ�{����(Schwarz-Christoffel
formula)���̷s�ɥR�i�i�C
��۴��Ӯa�j�����μƾǨt(
Applied MathematicsImperial College London)�F��-�J�ҭ}(Darren
Crowdy)�б¦b�O�άM�g�dzN�����o�F��}�ʶi�i�A�Ϩ�i�Q���Ω��������Ϊ��C�æb�̷s�@��(March-June 2007)�X�����m�C�����ǾǷ|�ƾǶi�i�n(
issue of Mathematical Proceedings of the Cambridge Philosophical
Society)���x�W�o���L��Υ˯�-�J�������Ҥ�{����(Schwarz-Christoffel
formula)���̷s�ɥR�i�i�C
19�@�������A���ƾǮa�X�O��s�X���Υ˯�-�J�������Ҥ�{����(Schwarz-Christoffel
formula)���ۦW�����A�o�H�i��O�άM�g����s�C���ƾǮa�B�u�{�v�M��Ǯa�̦Ө��A�O�άM�g�O�@
�ӭ��n�z�פu��A�b�ܦh��쳣�Q�s�x���ΡA�Ҧp�A�b��žǤ�������l�ΤW�Ū���y�Ҧ��i��ؼҡC�ثe�A�O�άM�g�ٳQ���Φb���g
�t�ά�ǨӴyø�H�����ϯ��g�Y�Τ��ǽ誺�������c�C�M�ӡA�ܤ�140�~�ӡA�o�Ӥ����u�A�Φb���]�t�էΩΪ̤��W�h�Ϊ��Ϊ��C
�p���J�ҭ}�б¹��o�Ӥ�{������}�ʸɥR�A�ϱo���i�A�Ω��H�e���������ҡC�Ҧp�b�u�~�W�A�p�G�@�����ݩΪ̨䥦���誺�Ϊ����褣�@�P�A�Ҧp�A�����t���t�@�ا���Ϊ̤@�ǤաA��Ӫ��M�g�u��������W�γ��C�p���ɥR�����᪺��{���N�i�H�b�@��²�檺��L�ΤW��o�ǽ������Ϊ��i��M�g�M���R�C
�@
Copyright ©�����u�@�{
all rights reserved.