怪店不怪--談數學歸納法

我們曾經討論過「怪店」的巧妙定價，店裡售價由顧客按著牆上佈告牌的步驟，自己決定價錢。步驟如下：

將蛋塔分成兩堆，將兩堆的蛋塔個數相乘得第一個乘積。
將第一堆和第二堆再分成兩堆（每堆至少一個），又可得到兩個乘積。
依此類推下去，直到每一堆剩下一個蛋塔為止。
將以上各乘積相加，這些乘積的和就是每盒蛋塔的價錢。

循上述步驟，為什麼付費一樣呢？

一場成功的骨牌遊戲，一定是從第1塊骨牌推倒第2塊開始，接下來就是第2塊推倒第3塊，...依此類推，並且在結束前的過程當中，沒有發生無法順利推倒下一塊的狀況。
假定我們找到一副骨牌，骨牌數是可數的，卻數不完，每一塊骨牌的次序編號與自然數是1對1的對應。但是要如何確定每塊骨牌都被推倒了呢？如果第1塊骨牌推倒第2塊開始之後，過程中都能確定下一塊骨牌被推倒，那麼就能確認整副骨牌倒了。這過程如同數學歸納法。

義大利數學家皮阿諾 (G. Peano) 致力於符號形式邏輯與基礎數學的研究，他在1889年以拉丁文印製一本小書，只有36頁，書名為《算數原理，以一個新方法表示》(The principles of arithmetic, presented by a new method)。這本書中將自然數(正整數)的一些性質抽象化而得到一組公設，利用這組公設並用邏輯演繹得到自然數的性質，我們稱這些公設為皮阿諾公設。皮阿諾把每一個自然數的下一個數稱為這數的「後繼元素」(successor)，用後繼元素的說法，皮阿諾公設如下:

一、 1 是自然數
二、每一個自然數有一個自然數作他的後繼元素
三、 1不是一個後繼元素
四、不同數不可能有相同的後繼元素
五、設 S 是 N(自然數；正整數) 的子集（部分集合），若 1 是 S 的元素，且S 中的每一個元素的後繼元素
也是 S 的元素，則 S 就是 N ，也就是「數學歸納法原理」。

當我們使用數學歸納法證明那些對所有自然數都成立的數學命題時，通常用 P(n) 來表示這個命題，並且採取下列步驟證明:
一、 P(1) 成立
二、假設P(n) 成立，由P(n) 成立，推得 P(n+1) 成立

命題︰「如果蛋塔有n個，依怪店的定價步驟，價錢P(n)=$\large\frac{n(n-1)}{2}$，其中 n >1。」

用數學歸納法證明上列命題是否正確。

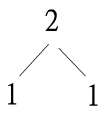
一、 n=2時，命題顯然成立

n=3時，命題也顯然成立

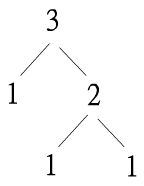
二、假設 n=k時，P(k)=$\large\frac{k(k-1)}{2}$成立。

因為，其中 k≧x≧1，

所以P(k+1)=x(k+1-x)+p(x)+p(k+1-x)=

x(k+1-x)+$\large\frac{x(x-1)}{2}$+$\large\frac{(k+1-x)(k-x)}{2}$=

$\large\frac{(k+1-x)(k+x)+x(x-1)}{2}$=$\large\frac{k(k+1)}{2}$=$\large\frac{(k+1)((k+1)-1)}{2}$

，因為n=k+1時，P(n)也成立。所以命題成立。
　

相關網頁: 怪店