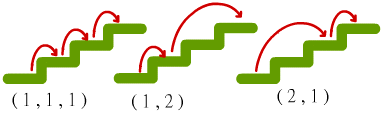
上樓梯一步一階或二階

如果樓梯只有一階，上樓梯的方法當然只有一種。
如果樓梯有兩階，你可以一步一階，也可以一步兩階，所以有二種方法。
如果樓梯三階以上，有幾種走法呢？
基於安全，不鼓勵一步跨三階，其實一步跨兩階也要小心。本文討論上樓梯的走法，限定一步走一階或兩階。
附圖是上三階樓梯的三種走法，分別以數對(1,1,1)、(1,2)、(2,1)表示。

樓梯階數是1,2,3,4,5,6，一步最多二階的樓梯走法有1,2,3,5,8,13(種)，如果上七階的樓梯，其走法是否有21種？上樓梯的走法數是否就是斐波拉契數列呢？

如果上n階樓梯的方法有f(n)種，顯然f(1)=1，f(2)=2。
上3階樓梯的方法有二種情況，(1)︰如果最後一步走一階，因為上樓梯前二階有f(2)種方法，所以有f(2)種方法。(2)︰如果最後一步是跨二階，則只有一種方法，即第一步上樓梯一階，所以有f(1)種方法。總共 f(3)=f(1)+f(2)。
上4階樓梯的方法有二種情況，(1)︰如果最後一步走一階，因為上樓梯前三階有f(3)種方法，所以有f(3)種方法。(2)︰如果最後一步是跨二階，因為上樓梯前二階有f(2)種方法，所以有f(2)種方法。總共 f(4)=f(2)+f(3)。
依此類推，上n階樓梯的方法有二種情況，(1)︰如果最後一步走一階，因為上樓梯前(n-1)階有f(n-1)種方法，所以有f(n-1)種方法。(2)︰如果最後一步是跨二階，因為上樓梯前二階有f(n-2)種方法，所以有f(n-2)種方法。總共 f(n)=f(n-2)+f(n-1)。

因為f(1)=1，f(2)=2，且 f(n)=f(n-2)+f(n-1)，n>2，所以{f(n)}是斐波拉契數列。