delesquar

縱橫刪 n 階數字方盤

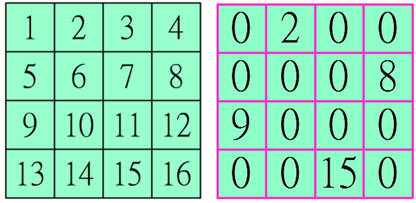
附圖，4×4方盤，1~16連續16個正整數由左而右，由上而下，依序填入方格中。
遊戲開始，先在方盤中任選一格，這方格內的數被保留下，但是跟它同列或同行的方格內的數被全部歸零。繼續遊戲，在方盤中任選非零的方格，直到剩下4格非零，其餘12格都歸零，遊戲結束。

無論你玩幾次上列遊戲，結束所留下的 4個數相加的總和都是 34。這是為什麼呢?

遊戲結束後留下的4個數不在同一列，也不在同一行。
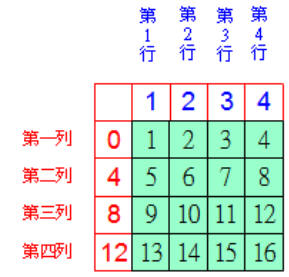
由下圖知方盤中，1 = 0+1，2 = 0+2，.....，10 = 8+2，11 = 8+3，......，15 = 12+3，16 = 12+4。
假設留下的4個數分別在第一列第 a 行，第二列第 b 行，第三列第 c 行，第四列第 d 行。其中，a、b、c、d彼此都不一樣大小，而且a+b+c+d=1+2+3+4=10。
因為第一列第 a 行的數等於 0+a，第二列第 b 行的數等於 4+b，第三列第 c 行的數等於 8+c，第四列第 d 行的數等於 12+d，所以( 0+a )+( 4+b )+( 8+c )+( 12+d )= 24+10= 34。這個 4×4方盤的對角線和也是34。

將遊戲推展到 n × n方盤 ( n≧1 )，將1~n由左而右，由上而下，依序填入方格中。
遊戲結束所留下的 n個數相加和= ( 0+n+2n+3n+4n+....+(n-1)n )+( 1+2+3+4+....+n )

= n×$\large \frac{(n-1)(1+(n-1))}{2}$+$\large\frac{n(1+n)}{2}$=$\large\frac{n(n^2+1)}{2}$。
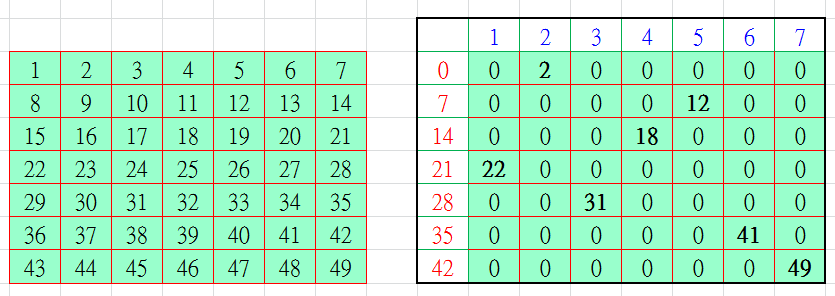
以7×7的 7階方盤為例，遊戲結束所留下的7個數的和=$\large\frac{7(7^2+1)}{2}$ = 175。

相關網頁:
縱橫刪 / 再談縱橫刪