由九九乘法表看連續整數立方和

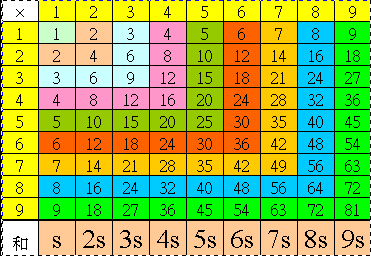
審視九九乘法表後，將第一欄各數相加和1+2+3+4+5+6+7+8+9 設定為 s，則其他各欄數字和依序是 2s、3s、4s、5s、6s、7s、8s、9s。所以表內數字總和是s+2s+3s+4s+5s+6s+7s+8s+9s=s×(1+2+3+4+5+6+7+8+9)=s² =(1+2+3+4+5+6+7+8+9)²。
我們可以換個角度審視九九乘法表，表裡2+4+2=2(1+2+1)=2×2²=2³ [註1]
，3+6+9+6+3=3(1+2+3+2+1)=3×3²=3³，......，9+18+27+36+45+54+63+72+81+72+63+54+45+36+27+18+9=9(1+2+3+4+5+6+7+8+9+8+7+6+5+4+3+2+1)=9×9²=9³。
因此，1³ + 2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³ =(1+2+3+4+5+6+7+8+9)²。

[註1]：圖解1+2+3+4+3+2+1

參考資料: 圖解連續整數的立方和