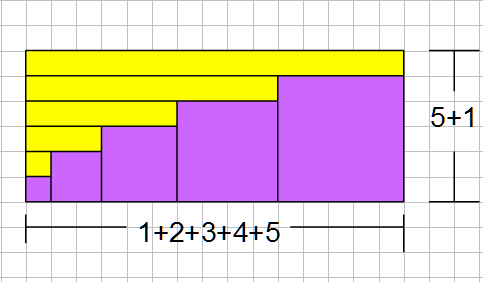
圖解連續正整數平方和公式

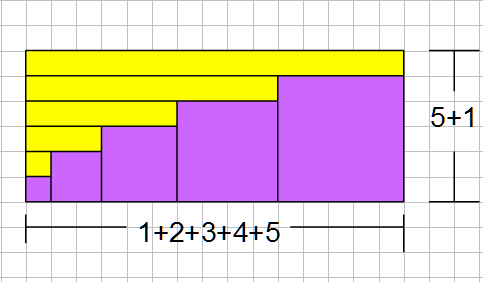
附圖，由5個正方形與5個小長方形組合成大長方形，5個正方形的邊長分別是1、2、3、4、5，5個小長方形的邊長規格分別是1×1、1×(1+2)、1×(1+2+3)、1×(1+2+3+4)、1×(1+2+3+4+5)，而大長方形的邊長規格是 (1+2+3+4+5)×(5+1)。
5個正方形的面積和等於 1²+2²+3²+4²+5²，5個小長方形的面積和等於1+(1+2)+(1+2+3)+(1+2+3+4)+(1+2+3+4+5)，大長方形的面積等於(1+2+3+4+5)×(1+5)，因此 1²+2²+3²+4²+5²＝(1+2+3+4+5)×(5+1)−[1+(1+2)+(1+2+3)+(1+2+3+4)+(1+2+3+4+5)]。
如果將附圖的正方形數目增加到n個，而且其邊長分別是1、2、3、‧‧‧‧‧‧、(n-1)、n，則根據上述規律可以推知
 1²+2²+3²+‧‧‧‧‧‧+(n−1)²+n²＝[ 1+2+3+‧‧‧‧‧+(n−1)+n ]×( n+1 )−[1+(1+2)+(1+2+3)+‧‧‧‧‧+(1+2+3+4+‧‧‧‧‧n)] 。

 $\small\displaystyle\sum_{k=1}^{n}{k^2}=\frac{n(n+1)}{2}\small(n+1)-\sum_{k=1}^{n}\frac{k(k+1)}{2}=\frac{n(n+1)}{2}(n+1)-\frac{1}{2}\sum_{k=1}^{n}k(k+1)=\frac{n(n+1)}{2}(n+1)-\frac{1}{2}\sum_{k=1}^{n}k^2-\frac{1}{2}\sum_{k=1}^{n}k$

 $\small\displaystyle\frac{3}{2}\sum_{k=1}^{n}{k^2}=\frac{n(n+1)}{2}(n+1)-\frac{1}{2}\sum_{k=1}^{n}k=\frac{n(n+1)}{2}(n+1)-\frac{1}{2}\frac{n(n+1)}{2}=\frac{n(n+1)}{2}(n+1-\frac{1}{2})=\frac{n(n+1)(2n+1)}{4}$

$\small\displaystyle\sum_{k=1}^{n}{k^2}=\frac{n(n+1)(2n+1)}{6}$

相關連結：圖解連續正整數的立方和

Copyright © 昌爸工作坊 All Rights Reserved.