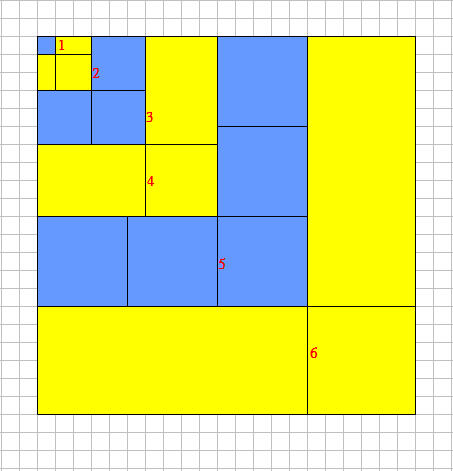
圖解連續正整數的立方和

參閱方格紙上的圖形可知
13 + 23
= 12+2(
1 ×
2 )+22
= ( 1+2 )2
( 13
+ 23
)
+33
= ( 1 + 2 )2+2[
( 1 + 2 ) ×
3 ] +32
= ( 1 + 2 + 3 )2
( 13 + 23 + 33 ) + 43 = ( 1 + 2 + 3 )2 + 2[ ( 1 + 2 + 3 ) × 4 ] + 42 = ( 1 + 2 + 3 + 4 )2
( 13 + 23 + 33 + 43 ) + 53 = ( 1 + 2 + 3 +4 )2 + 2[ ( 1 + 2 + 3 + 4 ) × 5 ] + 52 = ( 1 + 2 + 3 + 4 + 5 )2
( 13 + 23 + 33 + 43 + 53 ) + 63 = ( 1 + 2 + 3 + 4 +5 )2 + 2[ ( 1 + 2 + 3 + 4 + 5 ) × 6 ] + 62 = ( 1 + 2 + 3 + 4 + 5 + 6 )2
推廣
( 13 + 23 + 33 +‧‧‧‧‧‧+ (n-1)3 ) + n3 = ( 1 + 2 + 3 +‧‧‧‧‧‧+ (n-1) )2 + 2[ ( 1 + 2 + 3 ++‧‧‧‧‧‧+ (n-1) ) × n ] + n2 = ( 1+2+3+‧‧‧‧‧‧+n )2=(n(n+1)2)2
相關連結:圖解連續正整數平方和公式
Copyright ©
昌爸工作坊
All Rights Reserved.