數學角落

p.1

1950年德國數學家克拉芡提出一個奇妙有趣的問題，「任意一個自然數，如果是偶數，則用2來除；如果是奇數，則乘以3再加1。一直依循前述規則，最後一定得到數列：...4,2,1,4,2,1,4,2,1,.....」，這只是一個巧合呢？還是一個必然的規律呢？我們稱之為克拉芡猜想。

(1)、12，6，3，10，5，16，8，4，2，1，4，2，1，4，2，1，.....

(2)、17，52，26，13，40，20，10，5，16，8，4，2，1，4，2，1，4，2，1，.....

西洋棋手竟然敗給Chinook(契努克人工智慧程式)，2007年12月20日，美國《科學》雜誌公佈了2007年度科學研究十大突破，其中之ㄧ是"發現挑戰人類智力的電腦程式"。

從1989年開始，加拿大艾爾伯特大學（University of Alberta）的計算機科學家Jonathan Schaeffer和同事共同開發西洋跳棋人工智慧程式(Chinook)。有一些頂尖棋手的協助，Schaeffer利用啟發法（heuristics）將棋手的經驗編成計算機程式，透過約50部高效能電腦運算，研究5×10²⁰個跳棋位置，並時時監控程式並修正和更新，從而使"契克努"能夠在棋局獲得贏棋的先機，Jonathan Schaeffer和研究人員終於2007年4月完成了"契努克終極程式"，從此人類很難能贏人工智慧西洋棋。

參考資料:
http://www.sciencemag.org/cgi/content/abstract/1144079
http://www.cs.ualberta.ca/~chinook/

2008北京奧林匹亞運動會的游泳比賽中心水立方，它和鳥巢體育場堪稱北京奧林匹亞運動公園裡最醒目的兩座建築體。水立方的屋頂與牆面由多面體單元構成，每一單元包含六個十四面體和兩個十二面體。而這些多面體由正六邊形和邊長、角度不等的五邊形組成。

這種結構是都柏林三一學院的物理學家維埃爾(Denis Weaire)和費蘭(Robert Phelan)在1993年發現的。他們發現利用這樣繁複的方式所堆積成的多面體單元可以架構出表面積總和略少於在1887年由卡爾文爵士(Lord Kelvin)的所提出的十四面體。

高斯完成尺規作圖正十七邊形，並引以為傲。可是正七邊形卻不能利用無刻度的尺規來作圖，正七邊形的兩條不等長對角線長和一邊長具有性質:1/a=1/b+1/c，這性質可以利用托勒密定理證明它。

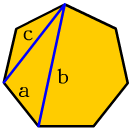
英國錢幣50便士採正七邊形設計，不同於常見的圓形，提高了防偽作用。而且該錢幣的曲線七邊形是等寬曲線，並不會造成使用投幣機的困擾。

參考資料：
星空燦爛的數學(Ⅱ)--托勒密定理(蔡聰明教授) / 正多邊形的世界(全任重教授) / 等寬曲線 / 尺規正十七邊形

今年(2007)是瑞士數學家歐拉(Euler)誕辰300周年，許多國家都舉辦紀念活動，瑞士政府也發行一套郵票紀念(如圖)。
數學領域處處可見歐拉(Euler)的名字─初等幾何的歐拉線、多面體的歐拉定理、立體解析幾何的歐拉變換公式、數論的歐拉函數、變分法的歐拉方程、複變函數的歐拉公式...。
歐拉是數學史上最多產的全才型數學家，Euler 與牛頓，萊布尼茲(Leibniz) 都是屬於新數學理論的開拓者。後人將歐拉(Euler)、高斯(Gauss)、黎曼(Riemann) 在數學的地位比喻為樂壇上的三 B：巴哈、貝多芬、布拉姆斯。雖然Euler在28歲時右眼失明，59歲時已經雙目失明，但是他一生勤奮寫下了886篇論文和多本書籍，平均每年寫出800多頁，這包括他在雙目失明後仍出版的書籍與口述發表的400多篇論文。後來，俄羅斯的彼得堡科學院為了整理他的著作，足足忙碌了47年。

1858年德國數學家、天文學家August Ferdinand Mobius和Johhan Benedict Listing兩人發現莫比烏斯帶（Mobius strip)，它是一種拓撲學結構，只有一個面，和一個邊界。可以用一個紙帶旋轉180度，再把兩端粘上就可以輕易製作出來。雖然其形狀已經數學家詳細闡述說明，卻一直沒有一個數學方程式能夠解開形狀是如何產生的以及其表面到底在那裡彎曲和如何彎曲的。因為紙條透過彎曲與扭轉所產生的壓力增加了紙條中儲存的能量，而"莫比烏斯帶如何將自身的能量最小化"，從1930年起就一直困擾著全球的力學科學家。

歷經近77年的努力，2007年7月15日，來自英國倫敦大學學院的非線性動力學家Gert van der Heijden和Eugene Starostin在 Nature Materials 發表一篇相關研究論文揭開了莫比烏斯帶的立體結構之謎。

歐拉─拉格朗日方程式在1989年被提出，也解決某些微分方程集，卻從未被用來解決莫比烏斯帶的難題。但是Gert van der Heijden和Eugene Starostin卻利用歐拉─拉格朗日方程式發展出一個數學方程式，可以準確預測不同長寬比例莫比烏斯帶的三維形狀，甚至到臨界極限，此時，莫比烏斯帶逐漸變平，最終成為一個等邊三角形。而莫比烏斯帶上各個位置的能量密度也因長寬比例相應改變，捲曲最劇烈的地方具有最高的能量密度，而平坦的地方能量密度最低。

新的研究成果對材料學、藥物開發等許多領域也具有重要意義。Eugene Starostin表示，它將有助於科學家理解一些生物分子和化學薄膜的架構。瑞士聯邦技術研究所的數學家John Maddocks認為研究中使用的方程式可適用於任何扭曲的長方形條帶，包括碳納米管。

玩具不倒翁穩定平衡時，重心和接地點的距離是最小，因此總要將底部加重。兩位數學家Gábor Domokos（匈牙利/布達佩斯技術學院）和 Péter Várkonyi （美國/普林斯頓大學）創造出的類似不倒翁形體，它如同不倒翁一樣總是可以回到原始的狀態，但是它並沒有被加重底部，而且內部是均勻的。他們稱這形體為『Gomboc』，該形體的表面是光滑的和曲線形的，可是他們仍不確定『Gomboc』是否可以是多面體。

延伸閱讀︰http://www.gomboc.eu/100.pdf

電線在兩電線桿之間懸垂成一曲線，我們稱這樣的曲線為「懸垂線」。
法國加拉比(Garabit)高架橋的拱軸線就是倒置的懸垂線，美國聖路易(St.Louis)拱門也是懸垂線。
y=(e^x+e^-x)/2的函數圖形就是懸垂線，乍看之下很像是拋物線，難怪連伽利略都看錯了。
巴西的Hercilio Luz橋的懸吊鍊就是拋物線。

延伸閱讀︰有點像，其實不同--懸垂線和拋物線

Thomas Heatherwick 被英國《泰晤士報》譽為英國最具創造力的藝術家。他在倫敦的Paddington Basin建造的開放式渡橋，伸展開時只像一般橋樑，可是捲曲後常令觀眾驚嘆不已! 這座長約40呎的大橋就像毛毛蟲一樣向上捲曲，直至在對岸幻化成為一座正八角柱體為止， Thomas Heatherwick 自許「我希望造一座有戲劇性的橋！」，顯然他是成功了。

瑞士在1957年發行尤拉(Euler)250周年誕辰紀念郵票，郵票上印上Euler在1748年所發表的公式，e^iΦ=CosΦ+iSinΦ。這個公式是三角函數和複數理論中最重要的公式，當Φ=π時，e^iπ+ 1= 0。Euler 非常熱愛這個公式, 宣稱這是最美麗的數學公式，並將這公式刻在皇家科學院的大門上。這公式包括有1和 0 ，分別是乘法和加法這兩個基本運算系統的單位元素，還有三個運算方法--加法、乘法和次方。另有兩個特別的數︰指數e 與圓周率π ，再加上虛數單位 i 。

賈恩茨考斯韋海岸（Giant's Causeway，巨人之路）位於北愛爾蘭貝爾法斯特西北約80公里處大西洋海岸。由總計約4萬根六角形石柱組成8公里的海岸。石柱連綿有序，呈階梯狀延伸入海。大約是6000萬年前太古時代火山噴發後熔岩冷卻凝固而形成的。賈恩茨考斯韋海岸1986年被列為世界自然遺產。自然界之中雪花、蜂窩等的形狀都是六邊形，自有其經濟原則。

延伸閱讀: 數學家稱蜂窩是世界上最省料的建築物