美妙的數

1. $\sqrt{7!+1}$=71
   
   

2. 123456789×2=246913578
   246913578×2=493827156
   493827156×2=987654312
   以上被乘數和乘積多是由1、2、3、4、5、6、7、8、9組成的數。
   
   

3.  2022 = 10+(9×8×7-6+5)×(4+3-2-1)
   2022 = 1234+5-6+789
   $2022=\dfrac{9+9}{9}\times(999+\dfrac{99+9}{9})$

    

4. 2!=2
   1! + 4! + 5!=145
   4! + 0! + 5! + 8! + 5!=40585

   
   

5. $\dfrac{1}{4}\times \dfrac{8}{5}=\dfrac{18}{45}$，$\dfrac{1}{2}\times \dfrac{5}{4}=\dfrac{15}{24}$，
   
     $\dfrac{2}{1}\times \dfrac{4}{5}=\dfrac{24}{15}$，$\dfrac{4}{1}\times \dfrac{5}{8}=\dfrac{45}{18}$。
   
   

6. 2021的倒轉數是1202，而2021²=4084441且1202²=1444804，其平方數互為倒轉數。
   2021和他的倒轉數相乘，乘積是一個回文數2429242，2021×1202=2429242。

    

7. 1×1!+2×2!+3×3!+4×4!+...+n×n!=(n+1)!-1
   
   

8. $\large\sqrt{2}$+$\large\sqrt{3}$≒$\large\pi$，$\large\pi^4$+$\large\pi^5$≒e⁶。
   
   

9. 37是第12個質數，73是第21個質數。37和73互為倒轉數，12和21互為倒轉數。
   73的二進位數碼1001001是迴文數。
   
   

10. AB 是拋物線的一割線，自AB的中點作平行於拋物線軸的直線交拋物線於C，阿基米得(Archimedes)計算弓形ACB面積時，得到無窮等比級數1+$\large\frac{1}{4}+\frac{1}{4^2}+\frac{1}{4^3}+....$，這是數學史上較早能計算出總和的無窮級數，也稱作阿基米得級數，級數收歛到$\large\frac{4}{3}$ 。證明 ACB弓形面積是三角形ABC面積的$\large\frac{4}{3}$ 倍。
    
    

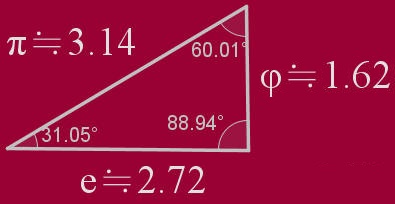
11. 圓周率 π ≒ 3.14，  歐拉數 e ≒ 2.72，  黃金比 φ ≒ 1.62。以π、e、φ的近似值為三邊長的三角形近似於30°-60°-90°的直角三角形。
    
    
    
    

12. 模糊數學大師--盧菲特·澤德(Lotfi Asker Zadeh)，1965年提出模糊集合和模糊邏輯，主要研究模糊邏輯的應用。他曾經提出「如何將0、1、2、3、4、…、9分成兩組，分別組成五位數字，並且這兩個數的平方數都是由0、1、2、3、4、…、9這10個數字所組成的十位數字。57321² = 3285697041，60984² = 3719048256。
    
    

13. 羅馬數字行列式的對稱美
    
    

     

     

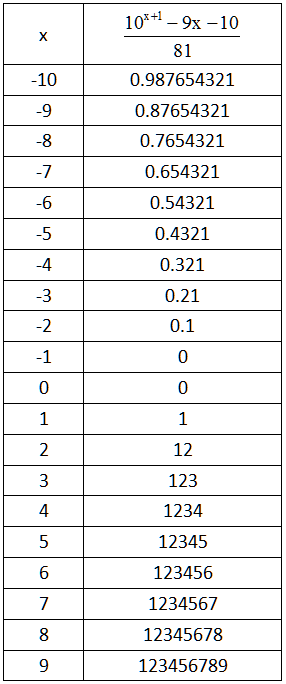
14. 美國加州高中(California high school)學生 Derek Hollowood 找到一個函數 f(x) =$\large\frac{10^{x+1}- 9x -10 } {81}$，當自變數x值由-10逐次加1遞增到 9，就會出現有趣的對應函數值。
    
    
    
    
    

15.  $\Large\frac{5}{34}$+$\Large\frac{7}{68}$+$\Large\frac{9}{12}$=1，$\Large\frac{1}{3 \times 6}$+$\Large\frac{7}{2 \times 4}$+$\Large\frac{5}{8 \times 9}$=1
    
    

16. 
    
    
    

17.   1738×4=6952，1963×4=7852
    
      138×42=5796，157×28=4396，159×48=7632，186×39=7254
      198×27=5346，297×18=5346，483×12=5796
    
    

18.   6! × 7! = 10!
    
    

19.   1!+4!+5! = 145
    
    
    

20.  
    
    
    
    
    

21. 
    

    
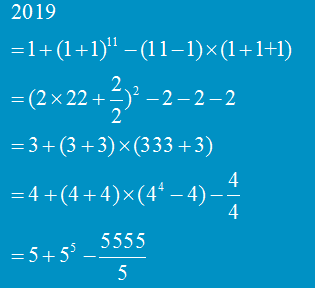
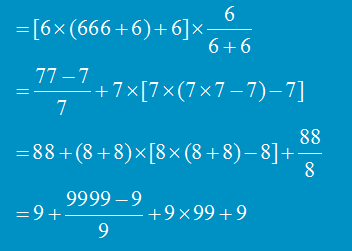
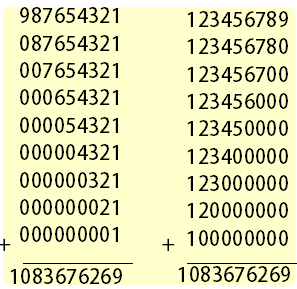
    循環節兩位兩位來看，出現00~97連續整數，但是最後兩位數是99而98。
    
    延伸閱讀：關於1/9801的循環小數表示

     
    
    

22.  
    
    
      延伸閱讀：從一個以16, 50, 33所寫成的等式談起
    
    
    

23.  
    10404 = 102×102，201×201 = 40401
    
    48972＝231×212，212×132＝27984
    
     25986＝213×122，221×312＝68952
    
    
    

24. 將1~15連續正整數，排列成 8，1，15，10，6，3，13，12，4，5，11，14，2，7，9，則相鄰兩數的相加和都是平方數。
    將1~16連續正整數，排列成 8，1，15，10，6，3，13，12，4，5，11，14，2，7，9，16，則相鄰兩數的相加和都是平方數。
    將1~17連續正整數，排列成 17，8，1，15，10，6，3，13，12，4，5，11，14，2，7，9，16，則相鄰兩數的相加和都是平方數。
    
    延伸閱讀：平方數列 (第53屆全國中小學科展)

     
    
    

25. 
    
    
    
    
    
    

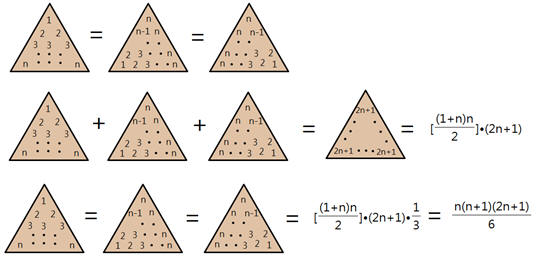
26.  $3^{3}+4^{4}+3^{3}+5^{5}=3435$
    
    
    

27.    
    
    
    
    
    

28. 2013=3×11×61，2013是三個相異質數的連乘積。而接續的2014、2015也都是三個相異質數的連乘積，2014=2×19×53，2015=5×13×31。
    試問三個連續整數都是三個相異質數的連乘積，還有哪些呢﹖
    

     
    

29. 
    
    
    
    

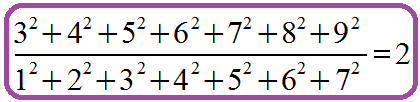
30.    (3+4)³ = 343，(4+0x9)⁶ = 4096，(7-5+9-3+7)⁵ = 759375
    
    
    

31.   14+28+57 = 99 ，142+857 = 999
      
      142857×142857=20408122449
      20408+122449 = 142857

     

32. 
    
    
    
    

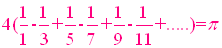
33.   365=10² +11² +12² = 13² + 14²

    　

      延伸閱讀：連續正整數平方和的有趣等式
    
    
    
    

34.   3²+4²=5² ，3³+4³+5³=6³
    
    
    

35.   一個算式的錯誤與正確就差在哪一「點」？
    

     

    
      想一想，如何在上式補上那一「點」，就可成為正確的算式了。

    
    

     
    
    
    
    

    ---

Copyright ©昌爸工作坊 all rights reserved.