台北區公立高中89學年度聯合招生

一、選擇題(有8題，每題5分，共40分)

  1. 下列何者不可作為一個三角形的三邊長？
    (A) 1,100,100 (B) 2,3,(C) ,,(D) 32,42,52

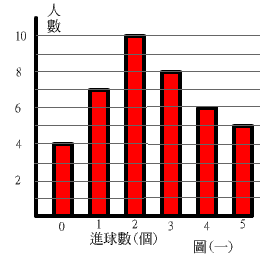
  2. 學期末，二年甲班學生進行投籃測驗，每人投5球，圖(一)為該班全體學生進球數的人數長條圖。如果從該班任意抽取一位學生，試問該生投進球數為圖(一)資料中的眾數的機率為何？
    (A) (B)(C)(D)

  3. 下列甲、乙、丙三個一元二次方程式，兩個根相等的有哪些？
    甲、3x2 - 6x+3= 0   乙、x2 -x+3= 0   丙、x2 -1= 0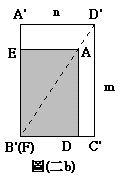
    (A) 甲、乙 (B)甲、丙 (C) 乙、丙 (D) 甲、乙、丙

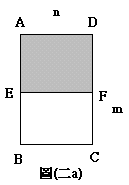
  4. 如圖(二 a)，有兩張全等的矩形影印紙ABCD與 A'B'C'D'，長為 m，寬為  n，E、F是、的中點，沿剪下矩形 EFDA，並疊到另一張影印紙 A'B'C'D'上，如圖(二 b)所示。若A在對角線上，則 m：n=
    (A) (B) (C) 1.4：1 (D) 1.7：1

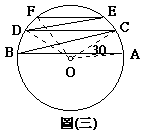
  5. 如圖(三)，圓O中，若//，//，，∠1：∠2=5：3，則∠DOF= (A) 9°(B) 18°(C) 15°(D) 20°

  6. 觀察兩條拋物線 y= 2(x+3)2 + 5和 y= - 2x2 - 12x - 13之圖形關係，下列何者正確？
    (A)開口方向相同(B)開口大小不同(C)對稱軸相同(D)頂點不同

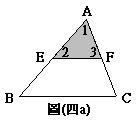
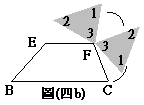
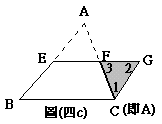
  7. 在圖(四a)中，有一個△ABC ，E、F是兩邊中點，沿將△ABC剪成兩塊，照圖(四b)的操作拼成圖(四c)。右下框的文字是創創對圖(四c)中，「為什麼EBCG是平行四邊形」所做的論述。你認為是否需要在空格(1)(2)中補上說明，才能使創創的論述更完整？


         

    創創說：圖(四c)中，三角形的與四邊形的等長，所以與能重合，(1)因此EBCG就是一個四邊形。另一方面，(2)//，又=(即)，因此EBCG是平行四邊形。

    (A) (1)不需補說明       (2)需補上：∠BEF+∠2=180°
    (B) (1)需補上：又∠BEF+∠3=180°      (2)不需補說明
    (C) (1)需補上：又∠BEF+∠3=180°       (2)需補上：∠BEF+∠2=180°，所以
    (D) (1)、(2)皆不需補說明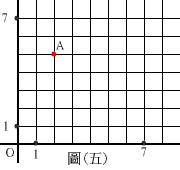 

  8. 圖(五)是坐標平面上的一個方格圖，圖中線段(縱橫各8條)的交點稱為格子點。A為給定的格子點，再方格圖中選擇三個格子點B、C、D，使得四邊形ABCD的面積最大。試問下列哪一條直線與此四邊形ABCD的一邊疊合？(必要時，可畫出此四邊形。)
    (A) X+Y-7=0  (B) 2X-5Y+21=0 (C) X-2Y+8=0 (D) X+2Y-12=0

二、填充題(有7題，每題6分，共42分)

  1. 化簡?

  2. 仁愛路某十字路口東西向的交通號誌只有綠、黃、紅三種，其燈量的時間比為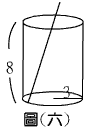綠：黃：紅= 8：1：6，那麼一天24小時中，「綠燈」亮的時間為 ___小時。

  3. 如圖(六)，有一個值圓柱狀的透明玻璃杯，由內部測得其底面半徑為3cm，高為8cm，今有一支12cm的吸管任意斜放於杯中，若不考慮吸管的粗細，則吸管路出杯口外的長度最少為 __cm。

  4. 等比級數前10項的和為___。(用最簡分數表示)

  5. 圖(七)是一個正方體，每個面上都寫有一個正整數，並且相對兩面所寫的兩個數字和都相等，如果20、49、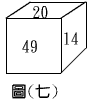14之對面所寫的數都是質數，依序為a、b、c，那麼a+b+c= ___。

  6. 守守班上有40位同學，她想再生日時請客，因此到超市花175元買果凍與巧克力共40個，若果凍每2個15元，巧克力每3個10元，則他買了多少個果凍？

  7. 台北市政府於今年七月一日起實施「垃圾費隨袋徵收」政策，垃圾袋的型號、規格及售價如表(一)所示，發現台北市政府再訂定每包售價十，有既定的規則。如果現在要按照這個規則製造一個新規格的垃圾袋，並以25個裝成一包出售，且設每個的容量為x公升，每包售價為y元，則x與y的關係式為___。
    表(一)

    型號 特小型 小型 中型 大型 特大型 超大型
    容量(公升/個) 5 14 33 45 76 92
    個數(個/包) 30 30 20 20 10 10
    售價(元/包) 75 210 330 450 380 460

三、計算、作圖題：(有4題，共38分)

  1. (1)因式分解 (x2-3x)+(x-3)2
    (2)若a為常數，解方程式[(x+a)2-3(x+a)]+[(x+a)-3]2=0(以a表示方程式的解x)

  2. 作圖：(保留作圖痕跡，但不必寫出作法)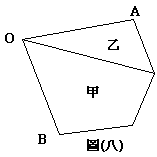
    圖(八)中，「四邊形甲」與「三角形乙」有一邊重合，。
    (1)在答案卷上畫出與「四邊形甲」全等的圖形。(可用任何工具作圖)
    (2)在圖(八)中，O點固定不動，將「三角形乙」依逆時鐘方向轉動，直到和重合。請在答案卷上畫出轉動完成後「四邊形甲」與「三角形乙」的組合圖。(請用尺規作圖，但是「四邊形甲」不必重畫，可用你在第(1)題所畫的圖。)

  3. 如圖(九)在坐標平面上，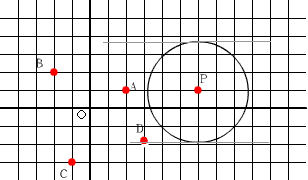
    (1)線段中，和者長度是？
    (2)試以P(6,1)為圓心，畫一個半徑為的圓。[註：原題無圖形圓O和切線]
    (3)當一個點的x坐標與y坐標都是整數時，我們稱它為整數點。承(2)，算出圓P內部的整數點的個數。
    (4)承(2)，寫出圓P的兩條平行於x軸之切線的方程式。

  4. 目前台北市政府推動警察減重計畫，男警的標準體重(公斤)為身高(公分)減去80在乘以0.7，女警的標準體重是身高減去70再乘以0.6。超過標準體重10%(不含)的為過重，超過標準體重20%(不含)的為過胖。
    (1)設一女警身高為165公分，若其體重為過重但不過胖，則其體重可能在什麼範圍？(可用超過、不超過、不足....等用語說明。)
    (2)有一男警身高為x公分，求其體重可達幾公斤仍不是過胖。(以x表示)
    (3)如果有一男警的體重，最重可達79.8公斤仍不是過胖，那麼他的身高為幾公分？

參考答案：

一、選擇題：(1).D  (2).A   (3).A   (4).B   (5).B   (6).C   (7).C   (8).B  
二、填充題：(1).    (2).  (3). 2   (4).    (5). 70  (6). 10   (7).
三、計算、作圖題： 
1.(1)   (X-3)(2X-3)  (2)  X= - a+3 或    
2. 略
3.(1) (2) 如上圖 (3) 21 (4) y=1+,y=1-
4.(1) 超過62.7公斤，不超過68.4公斤
   (2) 0.84x- 67.2
   (3) 175公分　

昌爸工作坊

回上一頁