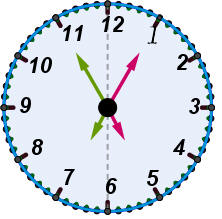
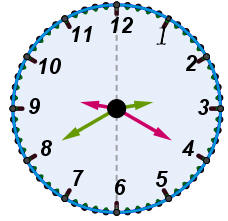
5點5分對稱於6點的時刻是6點55分
對稱時刻
定義:在圓形鐘錶上,如果時刻A和時刻B的算術平均數是6點,則彼此互稱為對稱時刻。
圓形鐘錶,僅考慮12小時制,鐘面上以6點為對稱軸,某時刻的對稱時刻是幾點幾分?
 |
 |
5點5分對稱於6點的時刻是6點55分 |
9點20分對稱於6點的時刻是2點40分 |
如果 y>0,則 x點y分對稱於6點的時刻是
(11-x)點(60-y)分。
如果 y=0,則 x點對稱於6點的時刻是 (12-x)點。
試問「在24小時制,在0點0分時針和分針重合,兩針夾角0°。那麼在一天裡時針和分針總共重合幾次?」
已知時刻對稱於6點,所以先思考時針和分針在0:00~6:00的重合次數。
因為鐘錶兩針指向x點y分,則時針和分針夾角 |$30x-\large\frac{11y}{2}$| (度) 或 360-|$30x-\large\frac{11y}{2}$| (度)。
如果x=0且兩針夾角0°,則 |$30\times 0-\large\frac{11y}{2}$|=0, 得 y=0,在0:00兩針重合。對稱時刻是12:00。
如果x=1且兩針夾角0°,則 |$30\times 1-\large\frac{11y}{2}$|=0, 得 y=$5\frac{5}{11}$,在1點$5\frac{5}{11}$分,兩針重合。對稱時刻是10點$54\frac{6}{11}$分。
如果x=2且兩針夾角0°,則 |$30\times 2-\large\frac{11y}{2}$|=0, 得 y=$10\frac{10}{11}$,在2點$10\frac{10}{11}$分,兩針重合。對稱時刻是9點$49\frac{1}{11}$分。
如果x=3且兩針夾角0°,則 |$30\times 3-\large\frac{11y}{2}$|=0, 得 y=$16\frac{4}{11}$,在3點$16\frac{4}{11}$分,兩針重合。對稱時刻是8點$44\frac{7}{11}$分。
如果x=4且兩針夾角0°,則 |$30\times 4-\large\frac{11y}{2}$|=0, 得 y=$21\frac{9}{11}$,在4點$21\frac{9}{11}$分,兩針重合。對稱時刻是7點$38\frac{2}{11}$分。
如果x=5且兩針夾角0°,則 |$30\times 5-\large\frac{11y}{2}$|=0, 得 y=$27\frac{3}{11}$,在5點$27\frac{3}{11}$分,兩針重合。對稱時刻是6點$32\frac{8}{11}$分。[註1]
由上述可知,在0:00~11:59時段裡兩針重合11次。因此12:00~23:59時段裡兩針重合11次。
所以在一天裡時針和分針總共重合22次。
[註1]:如果x=6且兩針夾角0°,則
|$30\times 6-\large\frac{11y}{2}$|=0, 得 y=$32\frac{8}{11}$,在6點$32\frac{8}{11}$分,兩針重合。對稱時刻是5點$27\frac{3}{11}$分。
參考資料:時針和分針的夾角
相關連結:對稱時刻 ggb
Copyright © 昌爸工作坊 all rights reserved.