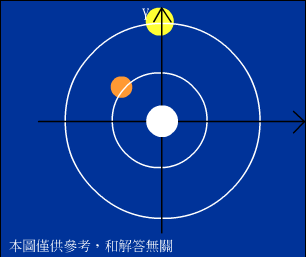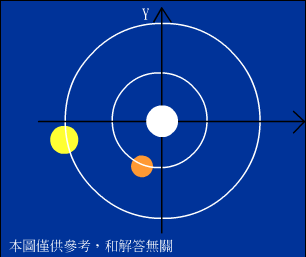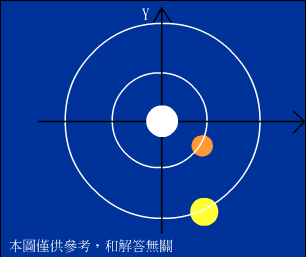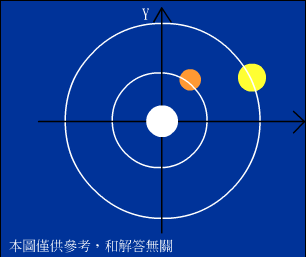
 「某恆星系中有甲、乙兩行星。假設兩者公轉軌道在同一平面上,且以恆星為圓心的同心圓。某時,甲行星在恆星與乙行星之間而成一直線。今在該平面上設定一座標如右圖。已知兩行星皆以逆時針方向運行,且公轉之週期比為2:7。試問下一次甲行星再度在恆星與乙行星之間成一直線時,是在第幾象限?」
(89年度大學聯考自然組數學試題)
「某恆星系中有甲、乙兩行星。假設兩者公轉軌道在同一平面上,且以恆星為圓心的同心圓。某時,甲行星在恆星與乙行星之間而成一直線。今在該平面上設定一座標如右圖。已知兩行星皆以逆時針方向運行,且公轉之週期比為2:7。試問下一次甲行星再度在恆星與乙行星之間成一直線時,是在第幾象限?」
(89年度大學聯考自然組數學試題)行星繞恆星
 「某恆星系中有甲、乙兩行星。假設兩者公轉軌道在同一平面上,且以恆星為圓心的同心圓。某時,甲行星在恆星與乙行星之間而成一直線。今在該平面上設定一座標如右圖。已知兩行星皆以逆時針方向運行,且公轉之週期比為2:7。試問下一次甲行星再度在恆星與乙行星之間成一直線時,是在第幾象限?」
(89年度大學聯考自然組數學試題)
「某恆星系中有甲、乙兩行星。假設兩者公轉軌道在同一平面上,且以恆星為圓心的同心圓。某時,甲行星在恆星與乙行星之間而成一直線。今在該平面上設定一座標如右圖。已知兩行星皆以逆時針方向運行,且公轉之週期比為2:7。試問下一次甲行星再度在恆星與乙行星之間成一直線時,是在第幾象限?」
(89年度大學聯考自然組數學試題)
因為甲、乙兩行星都是逆時鐘繞恆星運行,公轉的週期比是 2:7,假設甲行星繞恆星一周需 2x年,則乙行星繞行一周需 7x年。因為一圓周是360度,所以甲行星一年繞行$\frac{360}{2x}$度,乙行星一年繞行$\frac{360}{7x}$度。那麼下一次三顆星在一直線是什麼時候?
因為甲行星的週期較短,繞一圈的所需時間較少,所以下次三顆星在一直線應該發生在甲行星比乙行星多繞360度時。
假設y年後三顆星在一直線,則y( $\frac{360}{2x}-\frac{360}{7x}$ )= 360,得 y=$\frac{14}{5}x$。
也就是說,三顆星再次成一直線,甲行星需繞行$\frac{360}{2x}$×$\frac{14x}{5}$=504(度),即繞一圓周又144度。
而乙行星需繞行$\frac{360}{7x}$×$\frac{14x}{5}$=144(度),所以恆星、甲行星、乙行星再次在一直線時,甲行星、乙行星是在第二幾象限。
[註]:我們所在太陽系的行星軌道,經刻卜勒提出是橢圓,由牛頓利用數學方法證明軌道是橢圓.
Copyright ©昌爸工作坊 all rights reserved.