遊艇碼頭

觀光碼頭

某海洋島國想發展遊艇觀光，本島已經有一座合格的遊艇碼頭，計畫在劍島、盤島各增建一處遊艇停靠碼頭。劍島擁有直線型的海岸L，盤島則擁有圓形的海岸O。
規劃的旅遊行程是從本島A地搭船出發，先到劍島旅遊再到盤島觀光，則遊艇碼頭應選定在何處會有最便捷的動線(最短的航行距離)？

轉換成幾何問題︰「如何分別在直線L和圓O上找到C點和D點，使得AC+CD 值最小。」

作A點對稱於直線L的B點。
連接BO，BO與直線L交於C點;BO與圓O相交於D點。
則C點和D點即為遊艇碼頭所在地。

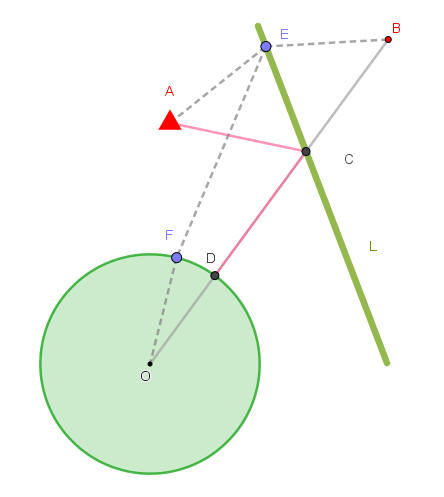
假設C點和D點不為所求，而是E點和F點為所求。
因為AE=BE，所以AE+EF+FO=BE+EF+FO＞BO。
因為BO=BC+CD+DO=AC+CD+DO，所以AE+EF+FO >AC+CD+DO。
因此AE+EF>AC+CD。矛盾，即假設錯誤。
所以C點和D點是遊艇碼頭的最佳地點。