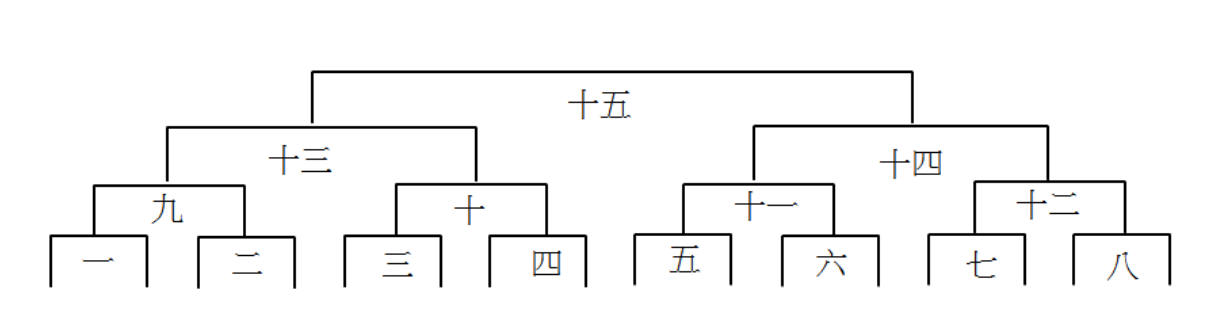
單敗淘汰賽程
單敗淘汰制競賽的參賽人次通常是2的次方, 能讓進入每一輪的選手都能打一場,沒有輪空的選手。
如果有2n人參加單敗淘汰的單打桌球比賽,則賽程有n輪,第一輪分成2n-1場,第二輪分成2n-2場,...,第n輪1場,每一場都是兩人對打。所有賽程需安排
2n-1+2n-2+2n-3+...+22+2+1 場比賽,n≧1。
因為1+2+4+....+2n-3+2n-2+
2n-1=$\large\frac{2^n-1}{2-1}$=2n-1,所有賽程需安排n輪總共2n-1場比賽。
例如:16人參加單敗淘汰的單打桌球比賽,因為16=24,整個賽程需安排4輪,總共16-1=15場比賽。

如果2n+a人參加單敗淘汰的單打桌球比賽,其中a是正數且1≦a≦2n-1,則第一輪需要淘汰a人,所以第一輪需要a場比賽,有2a人參賽,同時有2n-a人輪空。因為第一輪a場比賽完後,第二輪有2n人參賽,因此由第二輪起還要安排2n-1比賽,所以整個賽程需安排(n+1)輪,總共a+(2n-1)=(2n+a)-1場比賽。
例如:12人參加單敗淘汰的單打桌球比賽,因為12=23+4,所以第一輪需要淘汰4人,因此需要4場比賽,即第一輪有8人比賽,有4人輪空。第一輪比賽4場,第二輪起到第四輪賽程需安排23-1=7場比賽。整個賽程需安排4輪,總共4+7=12-1=11場比賽。
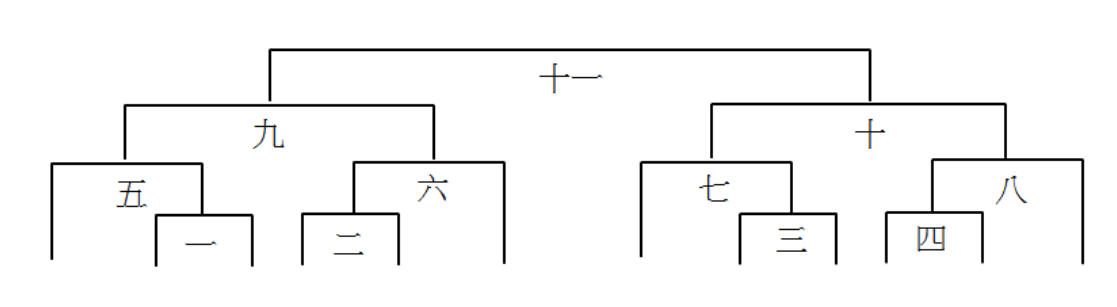
由上述可知,如果有x人參加單敗淘汰的單打桌球比賽,則賽程應安排(x-1)場比賽。
也可以作如是想,因為單敗淘汰,一場比賽就淘汰一人,冠軍只有一位。如果有x人參賽,則冠軍的出現需要有(x-1)人遭淘汰,所以需要(x-1)場比賽。
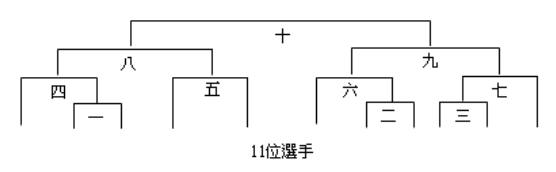
參考賽程:11人參加單敗淘汰的單打桌球比賽,4輪共10場比賽。
Copyright ©昌爸工作坊 all rights reserved.