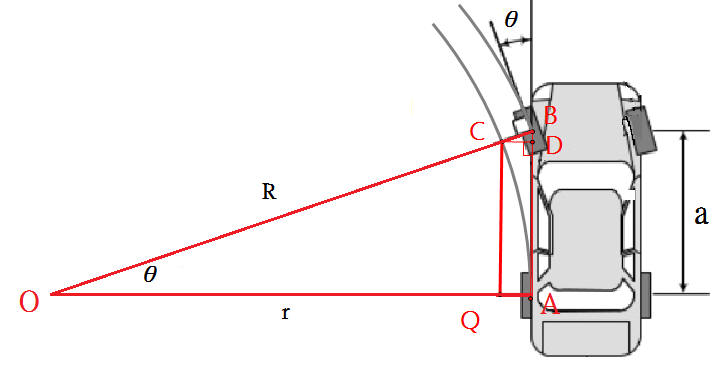
死亡半月彎的安全距離

前文「死亡半月彎(內輪差)」已經討論「車子的前、後輪軸距(a)越大，則內輪差越大；轉彎角度(θ)越大，則內輪差越大。」

為了避免進入死亡半月彎，行人和轉彎車子的安全垂直距離應該是車子軸距長的$\Large\frac{1}{3}$以上。為甚麼？

如圖，C點在後車輪軌跡上並且與車子的垂直距離是CD。直角三角形OAB，∠A=90°，C點在OB上，CD⊥BA 和BA相交於D點，CQ//BA交OA於Q點，則QA=CD。行人為了避免被車子擦撞或輾壓，行人和車子的垂直距離應該要大於CD，即行人的位置最好在CQ的左邊。

因為內輪差=BC=$R-r=a(\Large\frac{1-cos\theta}{sin\theta})$，已知 CD⊥BD，且∠BCD = θ，所以 CD = BC × cosθ =$a(\Large\frac{1-cos\theta}{sin\theta})$$cos\theta$，0° < θ < 90°。

令 $f(\theta)=\Large(\frac{1-cos\theta}{sin\theta})$$cos\theta$ , 則

$f(\theta)^{'}=\Large(\frac{1-cos\theta}{sin\theta})^{'}$$cos\theta+\Large(\frac{1-cos\theta}{sin\theta})$$cos\theta^{'}$ =

$\Large\frac{sin^{2}\theta-(1-cos\theta)cos\theta}{sin\theta^{2}}$$cos\theta+\Large(\frac{1-cos\theta}{sin\theta})$$ (-sin\theta)$ =

$\Large\frac{1-cos\theta}{sin\theta^{2}}$$cos\theta+cos\theta-1$ =$\Large\frac{cos\theta(1+sin^{2}\theta)-1}{sin\theta^{2}}$ =

$\Large\frac{cos\theta(1+1-cos^{2}\theta)-1}{sin\theta^{2}}$ = $\Large\frac{2cos\theta-cos^{3}\theta-1}{sin\theta^{2}}$

如果 $f(\theta)^{'}=0$ ，則 $ 2cos\theta-cos^{3}\theta-1=0$ ，得 $ (cos\theta^{2}+cos\theta-1)(cos\theta-1)=0$

因為0° < θ < 90°，所以 $cos\theta-1\neq0$ ， $ cos\theta^{2}+cos\theta-1=0$

因此得$\large cos\theta=\frac{-1+\sqrt{5}}{2}$， θ ≒ 51.8° ，大約 0.9弳度。

當 θ = 51.8° ， $f(\theta)$的最大值是0.30028，大約是$\Large\frac{1}{3}$。

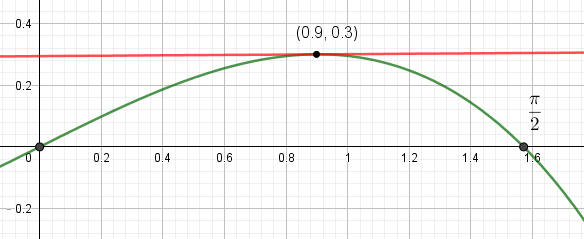
上圖是$f(\theta)=\Large(\frac{1-cos\theta}{sin\theta})$$cos\theta$的函數圖形，θ的單位是弳度，1弳度(弧度)=$\Large(\frac{180}{\pi})^{o}$，大約57°

當大型車轉彎51.8° 時，為了安全，行人與車子的垂直距離最好是車子軸距的$\Large\frac{1}{3}$以上。

雖然平時大型車轉彎大約是30°左右，f值小於0.3，但是基於安全考量，建議大家還是保持與車子的垂直距離是車子軸距的$\Large\frac{1}{3}$以上。

( 下表，軸距 a = 1 )

相關連結：死亡半月彎(內輪差)

微分公式：

$(fg)^{'}=fg^{'}+f^{'}g$，$\large(\frac{f}{g})^{'}=\large\frac{f^{'}g-fg^{'}}{g^{2}}$

$(sin\theta)^{'}=cos\theta$ , $(cos\theta)^{'}= -sin\theta$