72、69翻一倍法則

我們儲蓄金錢放在銀行n年，銀行採用一年計算利息一次，存錢一期(一年)後，將利息和本金當作下一期的本金計息，這種計息方式稱作複利。

例如，第一年存入銀行的本金是P元，年利率 r ％，則
第一年後的利息是 P × r ％，本利和=本金+利息=P+P×r ％=P( 1+r % )。

第二年的本金就是第一年後的本利和，則第二年後的利息是 P( 1+r % )×r ％，
本利和=P( 1+r % )+P( 1+r % )× r ％=P( 1+r % )×( 1+r % )=P( 1+r % )²。

第三年的本金就是第二年後的本利和，則第三年後的利息是P( 1+r % )²×r ％，
本利和=P( 1+r % )²+P( 1+r % )²×r ％=P( 1+r % )²×( 1+r % )=P( 1+r % )³。

直到n年約滿，可以擁有的本利和是P( 1+r % )ⁿ。

例如：

儲蓄本金100000元，年利率1.08%，複利計息，10年後的本利和是111340元，約為原來本金的1.1倍。

那麼，如果後來本利和是原來本金的2倍，則至少要儲蓄多少年？

試問：「採用複利計息，一年一期，如果n年約滿的本利和是第一年本金的2倍，則n應該是多少？」

假設P( 1+r % )ⁿ=2P，即( 1+r % )ⁿ=2，則n×ln( 1+r % )= ln 2，因此

n=$\large\frac{ln 2}{ln (1+r\%)}$ ...公式(1)

得知「若存入本金P元，年利率r %，採複利計息，在$\large\frac{ln 2}{ln (1+r\%)}$年後可以翻一倍成2P元。」

因為自然對數函數 ln (1+x)的泰勒級數展開式是 $\ x-\frac{x^2}{2}+\frac{x^3}{3}-...$，|x|<1。

當x很小時， ln (1+x)近似於 x。例如：ln (1+0.01)≒0.0099≒0.01。

所以當r%很小時，n=$\large\frac{ln 2}{ln (1+r\%)}$≒$\large\frac{ln 2}{r\%}$=$\large\frac{0.69}{r\%}$=$\large\frac{69}{r}$。( ln 2≒0.69 )

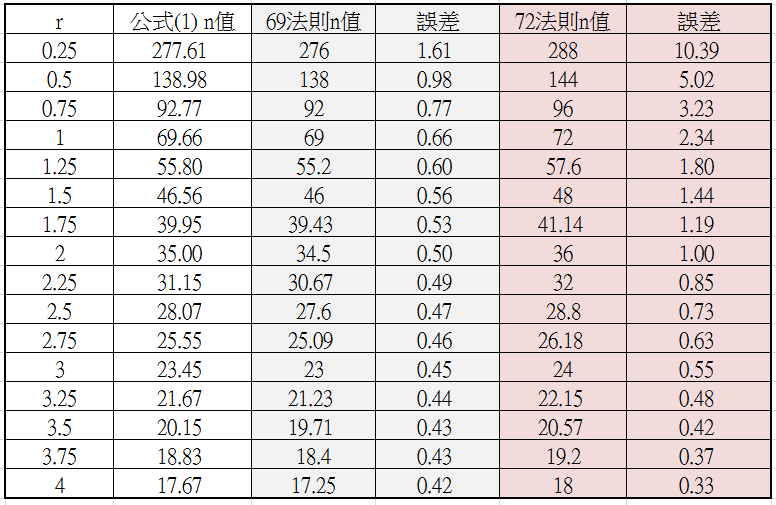
雖然目前大多數的人採用72法則估計投資翻倍的年資$\large\frac{72}{r}$，可是現在是低利率(1％-3％)的時期，顯然69法則($\large\frac{69}{r}$)的估計誤差比較小，可以參見下表。

例如：儲蓄本金100000元，年利率1.08%，複利計息，以69法則估計，$\large\frac{69}{1.08}$約64年後能有存款額200000元。

( 年利率 r ％，複利計息，n年翻倍，本金P元翻滾成本利和2P元 )