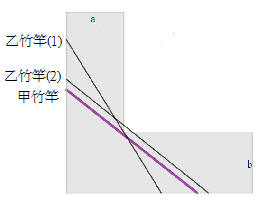
平舉竹竿通過直角彎道

「如圖，，直角彎道的兩側豎立高牆，直角彎道的道路寬分別是 a 與 b。有一個人想要平舉一支竹竿通過彎道，則這支直竿的長度最長是多少 ? (竹竿保持平行於地面且離地面高度不超過高牆高度)」

顯然，只需要討論竹竿在轉彎時，若竹竿的兩端接觸一側邊兩點，而且竹竿可接觸到另一側的轉角頂點，如圖，甲竹竿和乙竹竿(1)，它們是否能通過轉彎？

假設甲竹竿可以通過直角彎道，若其兩端點在彎道的側邊上，竹竿也可以接觸另一側的頂點。

如果乙竹竿(1)比甲竹竿長，且其兩端點在彎道的側邊上，並可以接觸彎道另一側的頂點。可以移動乙竹竿(1)成平行於甲竹竿的位置(乙竹竿(2))，因為乙竹竿(1)比甲竹竿長，顯然乙竹竿(2)和彎道另一側會有兩個交點，也就是說明它過不了彎道，因此甲竹竿的長的最小值就是問題所求。

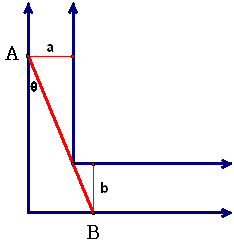
如圖，甲竹竿AB長等於$\Large\frac{a}{sin θ}+\frac{b}{cos θ}$ ，因為可以通過彎道，所以AB長應該小於等於$\Large\frac{a}{sin θ}+\frac{b}{cos θ}$ 的最小值。

 「求  $\Large\frac{3}{sin θ}+\frac{2}{cos θ}$ 的最小值?」是民國72年大學聯考數學試題，此題考倒大多數的高中學生。全國第24屆科學展覽出現一件數學作品，由嘉義女中吳素萍、林怡君、林溫慧三位同學在洪志雄老師的指導下榮獲高中組數學第三名，他們在坐標平面上討論$\Large\frac{a}{sin θ}+\frac{b}{cos θ}$ ，巧妙利用三角和柯西-史瓦茲不等式處理了「求$\Large\frac{a}{sin θ}+\frac{b}{cos θ}$ 的最小值?」。

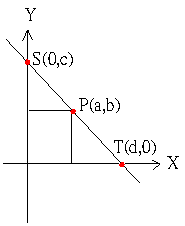
如圖，坐標平面上經過S(0，c)、T(d，0)兩點的直線方程式是 $\Large\frac{x}{d}+\frac{y}{c}$ =1 ，而且P(a，b)在直線上，所以 $\Large\frac{a}{d}+\frac{b}{c}$ =1 。

根據柯西-史瓦茲不等式，如果 α > 0，β > 0，則 (c²+d²)(α²+β²) ≧ (cα+dβ)²。...(1)

因為 (dβ+cα)($\Large\frac{a}{d}+\frac{b}{c}$) ≧ $(\sqrt{aβ}+\sqrt{bα})^2$，所以 dβ+cα ≧ $(\sqrt{aβ}+\sqrt{bα})^2$。...(2)

由(1)(2)可知ST=$\sqrt{c^2+d^2}$ ≥ $\large\frac{(\sqrt{aβ}+\sqrt{bα})^2}{\sqrt{α^2+β^2}}$。
當 (1)式等號成立時 c : d = α : β；當(2)式等號成立時 ，$\sqrt{dβ}:\sqrt{cα}$ = $\Large\sqrt{\frac{a}{d}}:\sqrt{\frac{b}{c}}$，得 $\Large\frac{c}{d}$ = $\Large\frac{\sqrt{bβ}}{\sqrt{aα}}$。

因為$\Large\frac{α}{β}=\frac{\sqrt{bβ}}{\sqrt{aα}}$，所以$\large\frac{a}{b}=\frac{β^3}{α^3}$，令α=$\large\sqrt[3]{bk}$，β=$\large\sqrt[3]{ak}$

因此當 c : d = α : β，且  $\sqrt{dβ}:\sqrt{cα}$ = $\large\sqrt{\frac{a}{d}}:\sqrt{\frac{b}{c}}$時，

ST=$\sqrt{c^2+d^2}$ = $\Large\frac{(\sqrt{aβ}+\sqrt{bα})^2}{\sqrt{α^2+β^2}}$=$\large\frac{\sqrt[3]{k}(\sqrt{\sqrt[3]{a^4}}+\sqrt{\sqrt[3]{b^4}})^2}{\sqrt[3]{k}(\sqrt{\sqrt[3]{b^2}+\sqrt[3]{a^2}})}$=$\large\frac{(\sqrt[3]{{a^2}}+\sqrt[3]{{b^2}} )^2}{(\sqrt{\sqrt[3]{b^2}+\sqrt[3]{a^2}})}$=$(\sqrt[3]{{a^2}}+\sqrt[3]{{b^2}} )^{\frac{3}{2}}$，

可得ST的最小值是$(\sqrt[3]{{a^2}}+\sqrt[3]{{b^2}} )^{\frac{3}{2}}$，

所以可以通過直角彎道的竹竿長度 ≦ $(\sqrt[3]{{a^2}}+\sqrt[3]{{b^2}} )^{\frac{3}{2}}$。

例如:直角彎道垂直的兩段路寬，分別是7公尺與9公尺。平舉22公尺的竹竿可以通過彎道，但是換成平舉23公尺的竹竿就無法通過彎道了。

延伸閱讀：「 p和q為正常數，0 < θ <  $\Large\frac{π}{2}$，$\Large\frac{p}{cos θ}+\frac{q}{sin θ}$最小值之求法及推廣」 (第24屆全國中小學科展)

■ 檢測 可以通過直角彎道的竹筏的長度 (ggb檔)