滾動架木板的圓柱

滾動架上木板的圓柱

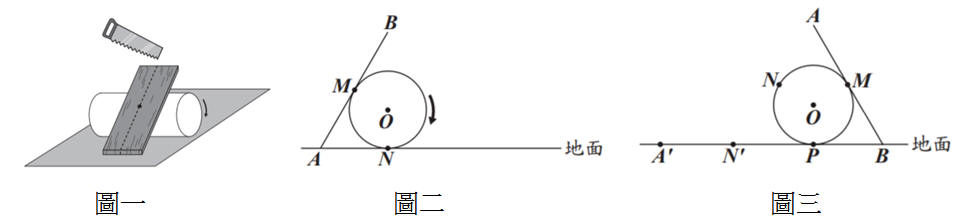
109年會考(補考)數學科試題非選擇題第2題。
「有個由實心圓柱和長方形木板組成的模型在水平地面上滾動，如圖 ( 一 ) 所示，在沿著圖中虛線做的垂直截面上，O 點為圓柱截面的圓心，M 點為木板AB 與圓 O 的固定點，也是 AB 的中點，而 N 點為圓 O 與地面的接觸點，如圖 ( 二 ) 所示，其中圓 O 半徑為 5，AB = 10$\sqrt{3}$。

今在沒有滑動的情況下，將圓 O 向右滾動，直到 B 點接觸地面為止，如圖 ( 三) 所示，其中 P 點為圓 O與地面的接觸點， A′、 N′ 兩點分別為圓 O 滾動前 A、 N 兩點在地面上的位置。」
在不計木板厚度的情況下，請根據上述資訊，回答下列問題︰
(1) 圖 ( 一 ) 中 ∠ MAO 的度數為多少?
(2) 判斷圖 ( 二 ) 中 N′P 與 AM，哪個線段長度較長，並詳細解釋或完整寫出你的理由。

[解]︰

(1) 因為 OM = 5，AM = 5$\sqrt{3}$，且∠OMA=90°，所以∠MAO=30°。

(2) 圖三，∠MOP=120°，且∠MON=120°，因此∠NOP=120°。
因為 N'P=$\small\overset{\frown} {NP}$，且$\small\overset{\frown} {NP}$=$\large\frac{120}{360}$$\times 2\pi\times 5$ =$\large\frac{2}{3}$$\pi\times 5$。而 AM = 5$\sqrt{3}$，因為$\large\frac{2}{3}$$\pi$>2>$\sqrt{3}$，所以N′P > AM。