昌爸工作坊-圓周率和CPU

圓周率和CPU

西元1761年朗伯特(Johann Heinrich Lambert，1728 - 1777)首先證明π是無理數(不能以分數表示)。他先證明「如果x是有理數，則tan(x)必為無理數」，因此「如果tan(x)是有理數，則x是無理數」。因為tan(π/4)＝1，所以π/4是無理數，π也必是無理數。西元1882年林德曼（Lindemann，1852-1939）證明π是超越數。滿足有理係數方程式的複數是代數數，而不是代數數的複數就是超越數。因此，古希臘著名三大幾何作圖之ㄧ「畫圓為方」也就不可能囉。

π是一個不循環的無限小數，拜當今先進高速速運算科技所賜，可以利用更超高精度的計算來逼近π。日本日立公司也認為通過計算圓周率，是有助於提升編譯器、數值計算和節點間通信的程式庫（Library）、磁記錄設備的輸入輸出性能調節以及提升長時間高速穩定的運算技術。西元1995年東京大學的D.Takahashi 及 Dr. Y.Kanada兩人合作設計一個可以計算π的程式Super Pi，它是利用 CPU 的浮點運算能力來計算圓週率的，目前被超頻玩家拿來用做測試系統穩定度和測試CPU運算所須時間。

西元2002年12月6日東京大學資訊基礎中心超級計算研究部門的金田康正教授正式發表，他們利用日立製作提供的超級電腦“SR8000/MPP”將π，3.14……持續不斷的計算到小數點後1兆2千億位，創造了圓周率計算的世界新紀錄。以前的紀錄也是由金田康正教授的團隊，在西元1999年9月所創造的2061億位。而這次計算改善並採用了由金田康正教授和日立共同開發的名為「分解有理數化法（DRM法）」的計算演算法。將位數一下擴大到約6倍。主要計算和驗算總共大約用了600個小時。其間曾停止過計算，而所有的計算是在11月24日完成的。π小數點後第1百萬位元的數字是2，第1兆2411億位的數字是5。

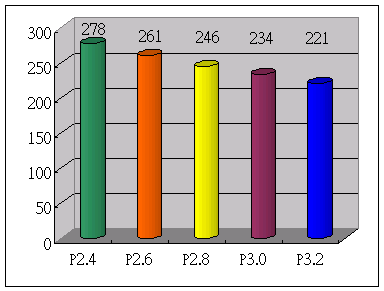
當Intel公司推出奔騰（Pentium）CPU時，就曾通過運行π的計算而找到的一個設計上的小問題。所以超高精度的π計算直到現在還是有其重要意義的。Super Pi這個程式最主要的目的是它只要利用個人電腦就可計算圓週率至小數點第33.5百萬位數，如果計算π至小數後419萬位來測試Pentium2.4G、2.6G、2.8G、3.0G、3.2G運算速度。結果3.2G領先了最慢的2.4約21%。而時間只用了221秒，還不到4分鐘。(參閱右圖)

　