切派餅

派的表面是圓形，切派都是由上向下切，切痕是圓的弦。不考慮派的厚度，所以沒有橫切的狀況。

因為要計算最多可以切下多少塊派，所以任意兩切痕不是平行，而且任意三切痕不會相交於一點。

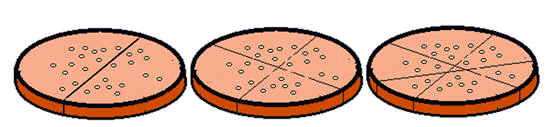
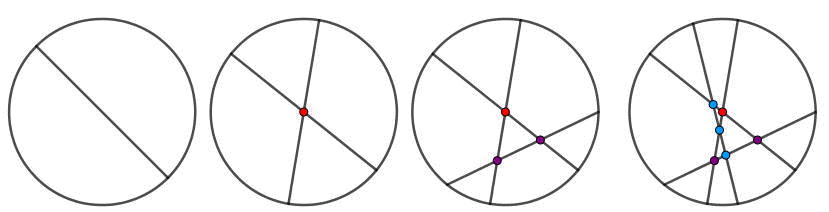
派一刀可以將派切成2塊，如果第2刀和第一刀的切痕不重合且有交點，則有一個交點，並且多切出2塊派，總共有2+2=1+(1+2)=4塊派。

如果第3刀和前二刀的刀痕都不重合且都有交點，則第3刀和前二刀的刀痕有二個交點，而且多切出3塊派，總共有1+(1+2+3)=7塊派。

如果第4刀和前三刀的刀痕都不重合且都有交點，則第4刀和前三刀的刀痕有三個交點，而且多切出4塊派，總共有1+(1+2+3+4)=11塊派。

依此類堆，如果第n刀和前(n-1)刀的刀痕都不重合且都有交點，則第n刀和前(n-1)刀的刀痕有(n-1)個交點，而且多切出 n 塊派，總共有1+(1+2+2+3+4+...+n)塊派。