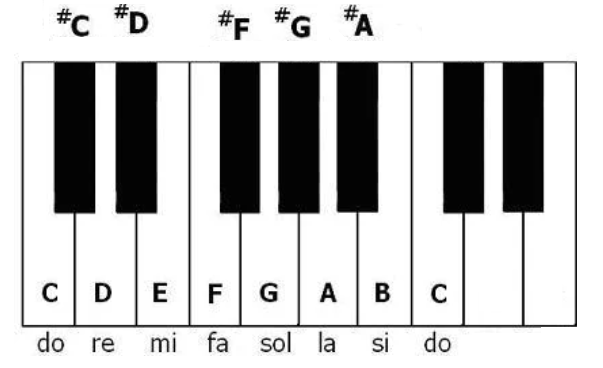
八度音和十二等程律

明代萬曆十二年（1584年）朱載堉提出「新法密率」，將Do~八度Do之間十二等分成12個半音，相鄰的半音頻率成固定倍率，這種定音律的方法稱作十二等程律或十二平均律。而朱載堉計算這個倍率的工具可不是現代的計算機而是大算盤，這大算盤有雙排八十一檔7珠共567子(附圖)。他能以珠算計算平方根和立方根，並計算$\sqrt[12]{2}$到小數24位，$\sqrt[12]{2}$近似於1.059463094359295264561825。朱載堉據此製作十二平均律律準和律管，影響西方的鋼琴鍵盤一組八度音有7個白鍵和5個黑鍵。

依照朱載堉的想法，Re的頻率是Do的$\sqrt[12]{2}$倍，Mi的頻率是Re的$\sqrt[12]{2}$倍，Fa的頻率是Mi的$\sqrt[12]{2}$倍，....，Si的頻率是La的$\sqrt[12]{2}$倍，而八度Do的頻率是Si的$\sqrt[12]{2}$倍，十二個半音的頻率成等比數列。

如果Do的頻率是1，則八度Do的頻率是2，將Do~八度Do的頻率列成13項的等比數列，公比是$\sqrt[12]{2}$。
因為等比數列的 第一項是1，第13項是2，且公比是r，則1×r¹²=2，因此r=$\sqrt[12]{2}$。

頻率的單位是赫茲(Hz)，表示每秒幾次週期。如果振動週期是$\frac{1}{10}$秒，則振動頻率是每秒10赫茲，A(La)的頻率是400赫茲。

$\sqrt[12]{2}$≒1.06，A#的頻率是A頻率的1.06倍，400×1.06=466(Hz)。

G#的頻率是A頻率的$\frac{1}{1.06}$倍，400×$\frac{1}{1.06}$=415(Hz)。