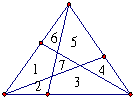
三刀割三角形的17
切三刀將三角形分成七小塊並不是難題,如附圖。但是要求切下原三角形面積的七分之ㄧ,就是一個挑戰了。

我們先認識「梅涅勞斯(Menelaus)定理,也稱作孟氏定理」:
E點在AB, D點在BC,且AD和CE相交於F點,則
¯AE¯EBׯBC¯CDׯDF¯FA = 1。
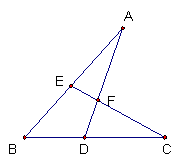
證明:
因為ΔAECΔBEC = ¯AE¯EB,ΔBCEΔCDE = ¯BC¯CD,而且 ¯DF¯FA = ΔDFEΔFAE =ΔDFCΔFAC =ΔDFE+ΔDFCΔFAE+ΔFAC =ΔCDEΔAEC ,因此¯AE¯EBׯBC¯CDׯDF¯FA =ΔAECΔBEC ×ΔBCEΔCDE×ΔCDEΔAEC = 1。
「將△ABC的三個邊三等分,並連接AD、BN、CE,則△FGH面積 = △ABC面積的17。」
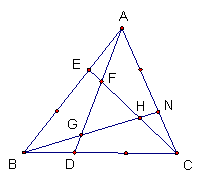
因為¯AE¯EBׯBC¯CDׯDF¯FA = 1,所以12×32ׯDF¯FA =1,因此¯DF¯FA =43。
因為△ACF=37△ACD=37×23△ABC=27△ABC。
同理可證,△ABG
= △BCH =27△ABC,所以△GFH = 17△ABC
Copyright ©昌爸工作坊 all rights reserved.