重差術求距離

《九章算術》出版於兩漢之間，將生活應用的數學問題編輯成冊，共九章。在「勾股」附測量的題目，曹魏的劉徽為「九章算術」作注時，將它列入第十卷，並測量法稱作重差術。到了唐初(西元263)，這些測量的題目被抽出來單獨成冊，因為該書第一題是測量海島的高度與遠近距離，因此書名《海島算經》，全冊只有九道題目，都是利用兩次、三次或四次觀測所得長度用來計算無法直接測量的高度和距離的問題。

《海島算經》第一題：

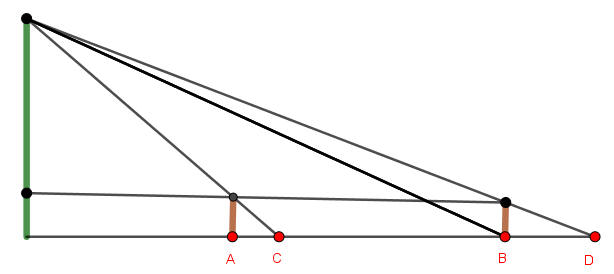
「今有望海島，立兩表齊高三丈，前後相去千步，令後表與前表三相直。從前表卻行一百二十三步，人目著地取望島峰，與表末三合。從後表卻行一百二十七步，人目著地取望島峰，亦與表末三合．問島高及去表各幾何？」

人站在陸地向遠眺望前方的海島，豎立兩支表竿(落地處分別是A和B)，兩表竿的高度k都是3丈，兩支表竿相距1000步，兩支表竿和海島成一直線。從前面的表竿A處倒退走123步，人蹲下使眼睛靠地表C處，使得眼睛、表竿頂和海島頂這三點在一直線。之後，從後面的表竿B處，倒退走127步，眼睛緊靠地表D處，使得眼睛、表竿頂和海島頂這三點在一直線。試問海島的高度是多少？海島和前表竿的距離是多少？

方法 :
k=3丈，AB=1000步，AC=123步，BD=127步。表竿高k乘以兩表竿距離AB，作為實(分子);並用相多(BD- AC) 為法 (分母); 除之，所得加上表竿高，即得海島的高度h。

島高 h=$\frac{k\cdot AB}{BD-AC}$+k

若求前表竿去島遠近者，以前表竿卻行(AC)乘以表間(AB)，作為實(分子)；(BD - AC)相多為法；除之，得島去前表里數。

前表竿去島遠 = $\frac{AC\cdot AB}{BD-AC}$

以上是老祖宗的做法，你可以利用三角形的相似性質解這道題。

參考資料：

中國數學攬勝 -- 傅溥/著 (幼獅文化事業公司)
中國古代數學簡史 -- 李儼/著 (九章出版社)
阿草的葫蘆 -- 曹亮吉/著 (九章出版社)