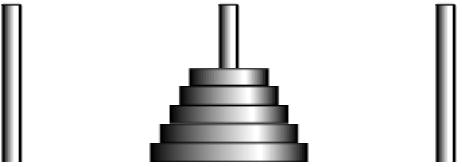
河內塔遞迴

法國數學家，愛德華·盧卡斯提出一個問題，大意如下︰

「有三根柱子，原先有n個圓盤套在同一根柱子，圓盤依大小由下而上，越上層則越小。如果完成移動n個圓盤套在其他的同一根柱子，需要移動的次數是多少 ﹖」

假設完成移動n個圓盤套在其他的同一根柱子，需要移動的次數是 a_n，顯然a₁=1。

總共移動1+1+1(次)= 2×1+1(次)，完成移動2層圓盤需要a₂(次)，a₂= 2×1+1= 2×a₁+1=3(次)。

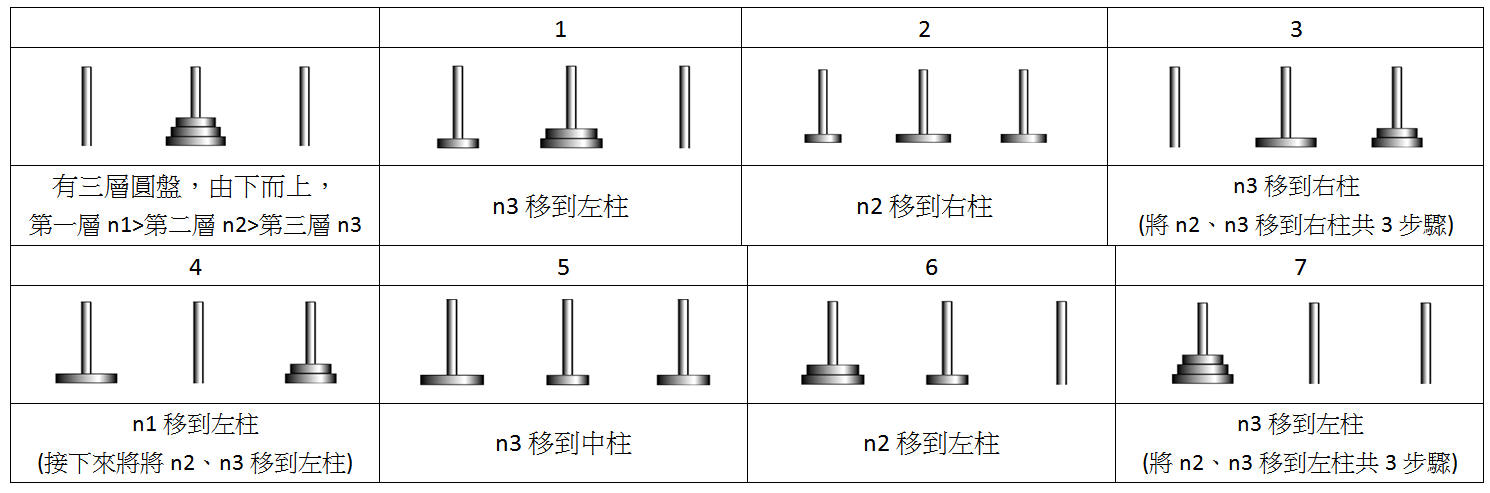
總共移動3+1+3(次)=2×3+1(次)，完成移動3層圓盤需要a₃(次)，a₃=2×3+1= 2×a₂+1=7(次)。

a₁=1
a₂=2×a₁+1
a₃=2×a₂+1=2×(2×a₁+1)+1=(2²a₁+2)+1
a₄=2×a₃+1=2×((2²a₁+2)+1)+1=(2³a₁+2²a₁+2)+1
.

a_n=2×a_n-1+1=(2^n-1a₁+2^n-2a₁+........+2³a₁+2²a₁+2)+1=2^n-1a₁+2^n-2a₁+........+2³a₁+2²a₁+2¹+2⁰= 2^n-1+2^n-2+........+2³+2²+2¹+2⁰= 2⁰+2¹+2²+2³.......+2^n-2+2^n-1= $\large\frac{2^n-1}{2-1}$=2ⁿ-1

另有想法，利用遞迴關係式 a_n=2a_n-1+1，a₁=1，求a_n的通式。
因為a_n=2a_n-1+1，所以a_n+1=2a_n-1+1+1，得a_n+1=2(a_n-1+1)。因此
a₂+1=2(a₁+1)         ...(1)
a₃+1=2(2a₂+1)       ...(2)
a₄+1=2(2a₃+1)       ...(3)
.
.
a_n+1=2(a_n-1+1)     ...(n-1)
上列各式相乘(1)×(2)×(3)×....×(n-1)，等號左右等量除、對消後，得a_n+1=2(a₁+1)×2^n-2。
因為a₁=1，所以 a_n+1=2²×2^n-2，得a_n=2ⁿ-1。

如果起始有n個圓盤在同一根柱子(A)，越上層的圓盤越小。您得將原先第二層到第n層的圓盤移到另外第二根柱子(B)，總共需移動2^n-1- 1次。之後，將原先的第一層圓盤(最大者)移至第三根空柱(C)上;再將柱子(B)的n-1個圓盤移到柱子(C)上，總共需移動2^n-1- 1次。完成整個過程需要移動的次數是(2^n-1- 1)+1+(2^n-1- 1)=2ⁿ - 1(次)。

「有三根柱子，原有n個圓盤套在同一根柱子，圓盤依大小由下而上，越上層則越小。欲完成移動n個圓盤套在其他的同一根柱子，則需要移動圓盤共2ⁿ-1次。」

相關遊戲︰河內塔