物流倉儲中心

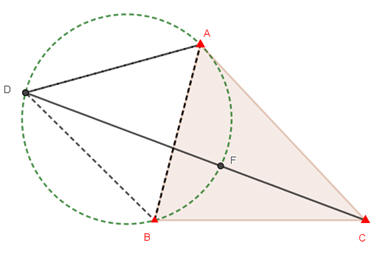
三角形區域的頂點分別是A地、B地、C地，△ABC的內角都是小於120°。有一家物流公司想在這塊三角形區域內尋找地點建立倉儲中心，考慮交通效益，希望這個地點分別到A地、B地、C地的距離和是最短的，則倉儲中心的最佳位置在哪裡。

首先以AB向外作正△ABD。
再作正△ABD的外接圓。
連接DC和△ABD的外接圓相交於F點，F點即倉儲中心的最佳位置。

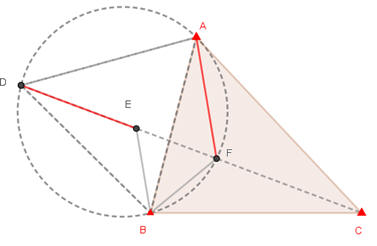
連接AF，並在DC上取DE = AF 。
連接△AFB和△DEB。
因為圓周角∠BAF和∠BDF所對的弧都是弧BF，所以∠BAF=∠BDF。
因為AF=DE，∠BAF=∠BDE，BA=BD(正三角形的邊)，所以△AFB和△DEB全等(SAS全等)，因此∠ABF=∠DBE且FB=EB。
在正△ABD內，∠DBE+∠ABE=60°，因為∠ABF=∠DBE，所以∠ABF+∠ABE=60°，因此∠FBE=60°。
因為FB=EB且∠FBE=60°，所以△FBE是正三角形。因此FB=FE。
綜合上述得知 FA+FB+FC=DE+EF+FC。
因為D、E、F、C四個點都在DC上，所以DE+EF+FC的最小值是DC長。
故F點即為倉儲中心的最佳位置。 (F點被稱作三角形的費馬點)