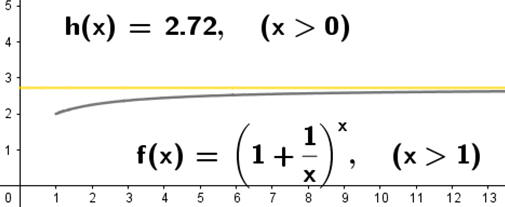
從複利本利和認識e

$(1+\frac{1}{n})^n$=$\small\left( \begin{array}{} n \\ 0 \end{array} \right) 1^n (\frac{1}{n})^0$+$\small\left( \begin{array}{} n \\ 1 \end{array} \right) 1^{n-1}(\frac{1}{n})^1 $+$\small\left( \begin{array}{} n \\ 2 \end{array} \right) 1^{n-2}(\frac{1}{n})^2$++$\small\left( \begin{array}{} n \\ 3 \end{array} \right) 1^{n-3}(\frac{1}{n})^3$+.......+$\small\left( \begin{array}{} n \\ n \end{array} \right) 1^0(\frac{1}{n})^n$=

1+n$(\frac{1}{n})$+$\frac{n(n-1)}{2!}(\frac{1}{n})^2$+$\frac{n(n-1)(n-2)}{3!}(\frac{1}{n})^3$+........+$(\frac{1}{n})^n$=1+1+$\frac{1-\frac{1}{n}}{2!}$+$\frac{(1-\frac{1}{n})(1-\frac{2}{n})}{3!}$+.......+$(\frac{1}{n})^n$

$\lim_{n \to\infty}(1+\frac{1}{n})^n$=1+1+$\frac{1}{2!}$+$\frac{1}{3!}$+.........

1+1=2

1+1++$\frac{1}{2!}$=2.5

1+1++$\frac{1}{2!}$+$\frac{1}{3!}$=2.6666.....

1+1++$\frac{1}{2!}$+$\frac{1}{3!}$+$\frac{1}{4!}$=2.7083333.....

1+1++$\frac{1}{2!}$+$\frac{1}{3!}$+$\frac{1}{4!}$+$\frac{1}{5!}$=2.716666.....

1+1++$\frac{1}{2!}$+$\frac{1}{3!}$+$\frac{1}{4!}$+$\frac{1}{5!}$+$\frac{1}{6!}$=2.71805555.....

1+1++$\frac{1}{2!}$+$\frac{1}{3!}$+$\frac{1}{4!}$+$\frac{1}{5!}$+$\frac{1}{6!}$+$\frac{1}{7!}$=2.718253968....

....

$\lim_{n \to\infty}(1+\frac{1}{n})^n$=2.71828182845904523536.........

1727年20歲的尤拉(Euler)在《近期加農砲彈發射時言之省思》手稿裡第一次使用字母e代表$\lim_{n \to\infty}(1+\frac{1}{n})^n$的極限值。1737年尤拉(Euler)出版《力學》，也提到e，這也是e首次出現在出版品，e=$\lim_{n \to\infty}(1+\frac{1}{n})^n$≒2.71828。

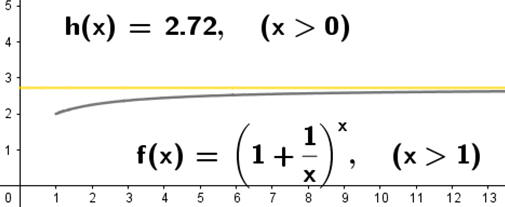
我們就從複利求本利和來認識 e。

所謂複利計算就是將本金存入銀行，以年利率計息，一年到期後，將本金與利息做為下一期的本金續存，仍用年利率計息。

如果本金是P，年利率是r，則一年後的本利和(本金+利息)=P(1+r)，續存一年後本利和=P(1+r)(1+r)=P(1+r)^2。如果共續存n-1次，則n年後的本利和是P(1+r)ⁿ。

假設本金是 1，年利率是 1，以複利計算，將1年分成n期計息，則1年後的本利和=(1+$\frac{1}{n}$)ⁿ。