滾動圓形錢幣

滾動銅板

兩個等值的圓形銅板，一個固定不動，另一個則繞著它的圓周滾動(不滑動)一周，則滾動的銅板會自轉幾周呢？

首先，假設圓形銅板的半徑長r，它在直線滾動(不滑動)一周，前進的路徑長或圓心移動的距離是否等於圓形銅板的圓周長呢？

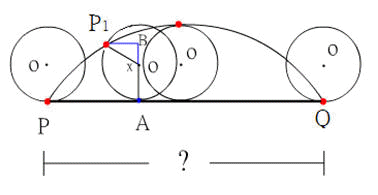
初始圓形O在直線上的切點P，若沿著直線向前滾動，OP旋轉x度，此時P點到達P₁點，切點A，∠P₁OA=x度。$\small\overset{\frown} {AP_1}$弧長 = PA長 = $\large\frac{x\pi r}{180}$ 。
直角三角形OBP₁，∠B=90°，∠P₁OB=(180-x)°，因此OB=r cos(180-x)°=-rcos x°，BP₁=r sin(180-x)°=r sin x°。
如果設定P點為坐標軸原點(0，0)，則P₁坐標是( $\large\frac{x\pi r}{180} $ -r sin x°，r - r cos x° )。
所以當銅板向前滾動一周和直線相切於Q點，則x=360度，此時Q點坐標是( $\large\frac{360\pi r}{180} $ -r sin 360°，r - r cos 360x° )= ( 2πr，0 )。
得知PQ長等於銅板的周長2πr，也等於銅板圓心所走的距離。總結來說，當銅板向前滾動一周，P點移到Q點，則線段PQ長等於銅板的圓周長，也是圓心移動的路徑長。

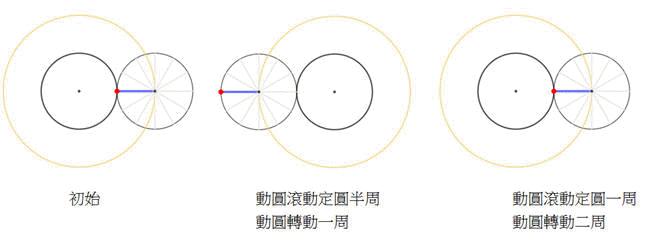
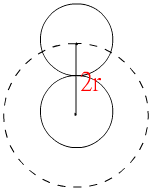
銅板繞著相同半徑r的固定銅板滾動(不滑動)一周，滾動銅板的圓心走了2π(2r) = 4πr長。因為固定銅板的周長是2πr，所以滾動銅板將自轉 4πr ÷ 2πr = 2 (周)。

「已知定圓O的半徑長R，動圓C的半徑長r，如果動圓C繞定圓O滾動一周，則動圓C會自轉 ( $\large\frac{R}{r}$+1 ) 周。」

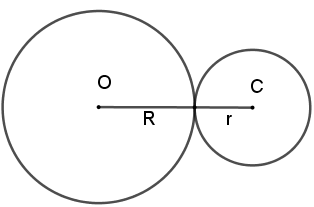
以O點為圓心，OC長為半徑的圓周長是 2π(R+r)。

如果動圓C繞定圓O滾動一周，則C點的路徑長 2π(R+r)。

因為動圓C自轉一周，其周長=2πr，所以

動圓C自轉周數=$\large\frac{2\pi(R+r)}{2\pi r}$= $\large\frac{R}{r}$+1