蜂窩

蜂巢

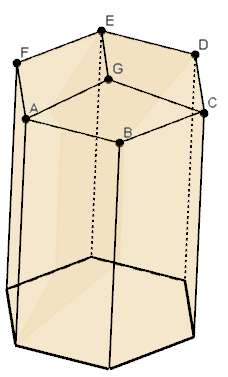
博物家達爾文曾讚嘆蜜蜂蜂巢是自然界的神奇建築，蜂巢的儲存室是六角柱，柱體朝外的一面是正六邊形，柱體的底部有3個全等的菱形。附圖，菱形ABCD、菱形CDEG、菱形EGAF，∠AGC=109°28'，∠GCB=70°32'。 ( 1° = 60' )

人們總是疑問蜂窩為什麼不呈三角形、正方形或其他形狀呢？隔牆爲什麽是平面，而不是曲面呢？

西元前180年，古希臘數學家Zenodorus證明出：
(1) 周長固定的n邊形，以正n邊形的面積最大。而且n越大，面積越大。
(2) 周長固定時，圓面積大於所有正多邊形。

古埃及人早知道唯有正三角形、正方形、正六邊形，能各自舖成一平面。

1712年瑞士數學家Samuel Konig 在博物學家Reaumur的請託下，證明：
「給定正六角柱，底部由三個全等菱形組成，最省材料的做法是，菱形兩鄰角分別是109°26' 和70°34'，如此在固定容積下，可有最小表面積」。法國天文學家 G.F. Maraldi實際測量菱形的相鄰角度，結果是109°28' 和 70°32' ，這和Samuel Konig的證明僅相差2'。

1943年，匈牙利數學家陶斯認為在所有緊密相連的正多邊形，正六邊形的周長是最小的，然而他沒有對此觀點提出證明。如果多邊形的邊是曲線時，又會發生什麽情況呢？

四世紀希臘數學家貝波司提出的《蜂窩猜想》︰蜂窩的優美形狀是自然界最有效經濟的建築代表。我們所見到的呈六邊形截面的蜂巢是蜜蜂採用最少量的蜂蠟所建造的。蜂巢每一個儲存室都是六面柱體，而蜂蠟牆的總面積和蜂巢的截面有關。由此引出一個數學問題︰「尋找面積最大而周長最小的平面圖形。」

1999年9月美國數學家托馬斯・黑爾斯（Thomas Hales）證明了《蜂窩猜想》。

2001年美國數學家托馬斯・黑爾斯（Thomas Hales）提出補充證明「在相同面積的區域，最佳覆蓋的圖形的周邊無論是曲線向外突還是向內凹，由許多正六邊形組成的圖形的周長最小」。

參考資料：數學的發現趣談--蔡聰明著 --三民書局