不等臂天平的麻煩

阿丹的藥材行使用的天平跟別人不同，天平的兩臂長度不一樣。客人上門時，他提供二種不同的稱重計價方式，由顧客自己選擇。已知不等臂天平，左臂10公分長，右臂20公分長。

第一種計價方式︰
「將藥材分成等重的兩份，一份放入左盤，砝碼放入右盤，不等臂天平平衡；另一份放入右盤，砝碼放入左盤，不等臂天平平衡。然後以兩次稱重的砝碼總重量計價」。

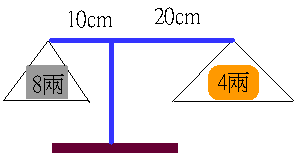
若藥材A放右盤，左盤放8(兩)的砝碼，不等臂天平會平衡，A應該重(8×10)÷20=4(兩)。

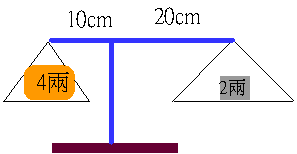
若藥材B放左盤，右盤放2(兩)的砝碼，不等臂天平會平衡，B應該重(2×20)÷10=4(兩)。
以上二次秤法，等重A和B的總重4+4=8(兩)，但是使用的砝碼總重8+2=10(兩)。砝碼總重大於物品總重。

顧客得用10兩重的藥材費用購買8兩重的藥材，顧客被阿丹占便宜了。

第二種計價方式︰
「按照顧客欲買的藥材重量，砝碼放左盤，藥材放右盤，砝碼重是欲購藥材重的一半。砝碼改放右盤，藥材放左盤，砝碼重還是欲購藥材重的一半。然後以兩次稱重的砝碼總重量計價」。

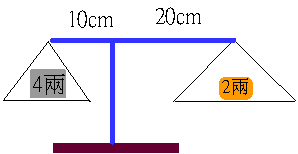
若顧客買8兩藥材，8÷2=4(兩)，阿丹將4兩重砝碼放左盤，藥材放右盤，藥材重(4×10)÷20=2(兩)，不等臂天平才會平衡。
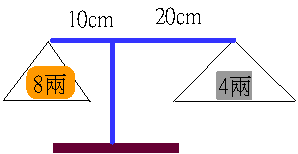
阿丹將4兩重砝碼放右盤，藥材放左盤，藥材重(4×20)÷10=8(兩)，不等臂天平才會平衡。
以上二次秤法，A和B的總重2+8=10(兩)，但是使用的砝碼總重4+4=8(兩)。砝碼總重小於物品總重。

顧客只用8兩重的藥材費就買到10兩重的藥材，顧客占便宜了。

如果鎮上所有人都知道這個秘密，而阿丹還不換掉不等臂天平，或者再想更好的計價方式，則他可要吃虧到關店了。

不等臂天平的左臂長a 公分，右臂長b公分，假設 a < b 。
狀況一，顧客欲買 2x 兩藥材，由槓桿原理知右盤需要$\frac{bx}{a}$兩的砝碼，左盤x 兩藥材，才能使不等臂天平平衡；左盤需要$\frac{ax}{b}$兩的砝碼，右盤x 兩藥材，才能使不等臂天平平衡。兩次秤法，砝碼總重x($\frac{b}{a}$+$\frac{a}{b}$)兩。

因為a≠b，所以 (a－b)²= a²－2ab+b² ＞ 0，因此 a²+b² ＞ 2ab ，即$\frac{a}{b}$+$\frac{b}{a}$>2。
所以狀況一的砝碼總重x($\frac{b}{a}$+$\frac{a}{b}$)兩大於2x兩重，這時若用砝碼總重計價，當然是對買方不利的。

而狀況二是先以x兩的砝碼分別放入左右盤去稱取藥材，這樣所稱得的藥材總重是x($\frac{b}{a}$+$\frac{a}{b}$)兩。
因為x($\frac{b}{a}$+$\frac{a}{b}$)>2x，所以顧客以少買多，當然是對買方有利的。