 四大文明古國之一的古巴比倫位於現今的中東伊拉克。美國耶魯大學(Yale
University)收藏很多古巴比倫泥板(西元前2000年~西元前1600年)。當中一塊泥板(編號YBC
7289)存在以楔形文字書寫的數字,考古學者認為這塊泥板大約存在於西元前18世紀的古巴比倫漢謨拉比國王時期,大約夏朝大禹時期。
四大文明古國之一的古巴比倫位於現今的中東伊拉克。美國耶魯大學(Yale
University)收藏很多古巴比倫泥板(西元前2000年~西元前1600年)。當中一塊泥板(編號YBC
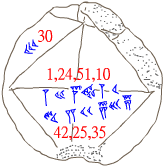
7289)存在以楔形文字書寫的數字,考古學者認為這塊泥板大約存在於西元前18世紀的古巴比倫漢謨拉比國王時期,大約夏朝大禹時期。泥板上有一個正方形和兩條對角線,如右圖,正方形的邊上的楔形文字是30,對角線附近有兩組楔形文字,分別是「 1,24,51,10」和「42,25,35」。
泥板上 $\sqrt{2}$
 四大文明古國之一的古巴比倫位於現今的中東伊拉克。美國耶魯大學(Yale
University)收藏很多古巴比倫泥板(西元前2000年~西元前1600年)。當中一塊泥板(編號YBC
7289)存在以楔形文字書寫的數字,考古學者認為這塊泥板大約存在於西元前18世紀的古巴比倫漢謨拉比國王時期,大約夏朝大禹時期。
四大文明古國之一的古巴比倫位於現今的中東伊拉克。美國耶魯大學(Yale
University)收藏很多古巴比倫泥板(西元前2000年~西元前1600年)。當中一塊泥板(編號YBC
7289)存在以楔形文字書寫的數字,考古學者認為這塊泥板大約存在於西元前18世紀的古巴比倫漢謨拉比國王時期,大約夏朝大禹時期。
泥板上有一個正方形和兩條對角線,如右圖,正方形的邊上的楔形文字是30,對角線附近有兩組楔形文字,分別是「
1,24,51,10」和「42,25,35」。
古巴比倫人採取60進位制,所以「1,24,51,10」,在十進位制就是1$+\frac{24}{60}+\frac{51}{60^2}+\frac{10}{60^3}=\frac{30547}{21600}$≒1.4142130≒$\sqrt{2}$。
而「42,25,35」 在十進位制是42$+\frac{25}{60}+\frac{35}{60^2}=\frac{30547}{720}$。
因為30
× $\frac{30547}{21600}$
= $\frac{30547}{720}$,所以30是正方形的邊長,而42$+\frac{25}{60}+\frac{35}{60^2}$是對角線長。原來泥板記錄「正方形的邊長乘以$\sqrt{2}$等於對角線的長度」。
但是有一些數學家則認為正方形的邊上寫的數字30可能是小數部分,也就是說正方形的邊長是$\frac{30}{60}$=0.5。
對角線長附近的「42,25,35」應該是
$\frac{42}{60}+\frac{25}{60^2}+\frac{35}{60^3}$=$\frac{30547}{43200}$≒0.707106481,大約就是$\sqrt{2}$的一半。這塊泥板記錄「邊長為0.5的正方形的對角線長是$\sqrt{2}$的一半」。
不管哪個說法,都足以證明古巴比倫人早在西元前2000年~西元前1600年就已經會運用古希臘的數學家畢達哥拉斯在西元前560年~西元前480年才提出來的的畢氏定理了。
[參考資料]:
古巴比倫楔形文字與十進位數字的對應表

相關網頁:
配方解二次方程的濫觴
Yale University Babylonian Collection
Copyright ©昌爸工作坊 all rights reserved.