A系列紙張與白銀矩形

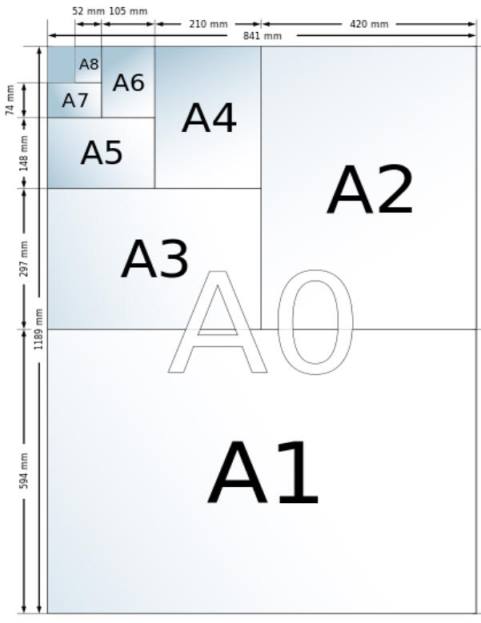
A系列紙張與白銀長方形

「是否存在長方形紙張，沿著長邊對摺成長方形後，再沿著新長方形的長邊對摺成長方形，而且這些長方形都是相似形呢 ?」

平時，我們使用印表機列印或掃描影印，所使用的A4紙就可以滿足上列條件。

將一長方形的紙張沿著長邊對摺成原來的一半﹐如果對摺後的長方形和原來的長方形是相似的，則稱這種長方形為白銀長方形，A4紙就是白銀長方形。

白銀長方形的長 x，寬 y，則 x：y＝y：$\Large\frac{x}{2}$，因此 x²＝2y²，x：y＝$\sqrt{2}$：1，所以白銀長方形的長寬比是$\sqrt{2}$：1。

ISO 216是國際標準化組織（ISO）所定義的紙張尺寸國際標準。A系列紙張的長寬比是$\sqrt{2}$：1，定義A0長1189公厘，寬841公厘，面積大約0.999949平方公尺≒1平方公尺。
將A0紙沿著長邊對摺一半，可得A1紙；將A1紙沿著長邊對摺一半，就是A2紙；將A2紙沿著長邊對摺一半，就是A3紙；將A3紙沿著長邊對摺一半，就是A4紙。An紙沿著長邊對摺一半，就是A(n+1)紙，n＝0~9。

如果從A系列任選不同大小的紙張，那麼他們都是相似形。

	A0	A1	A2	A3	A4	A5	A6	A7	A8	A9	A10
長(mm)	1189	841	594	420	297	210	148	105	74	52	37
寬(mm)	841	594	420	297	210	148	105	74	52	37	26

甲是長寬比$\sqrt{2}$：1的白銀長方形，假設寬是x，長是$\sqrt{2}$x。

從甲裁掉一個最大的正方形，即裁掉邊長x的正方形，得長方形乙。

長方形乙長x，寬($\sqrt{2}-1$)x，長寬比值是$\Large\frac{1}{\sqrt{2}-1}$＝$\sqrt{2}+1$。

從乙裁掉一個最大的正方形，得長方形丙，其長與寬的比值是$\Large\frac{2-\sqrt{2}}{\sqrt{2}-1}$=$\sqrt{2}$，所以甲和丙是相似形。

如果從丙裁掉一個最大的正方形，得長方形丁，其長與寬的比值是$\Large\frac{\sqrt{2}-1}{3-2\sqrt{2}}$=$\sqrt{2}$+1，所以丁與乙相似形。

$\sqrt{2}$+1≒2.414213562 被稱為白銀分割率，記做δ_S。如果a與b兩個數的比值是δ_S，則滿足$\Large\frac{2a+b}{a}$=$\frac{a}{b}$。

如果用繁分數表示δ_S，則

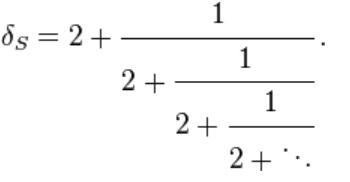
定義佩爾(Pell)數，第1個佩爾數P₁＝0，第2個佩爾數P₂＝1，當n≧3，第n個佩爾數P_n＝2P_n-1+P_n-2。佩爾(Pell)數形成佩爾(Pell)數數列，首項0，第一項是1，第三項開始每項都是前一項的兩倍加上前二項。佩爾數數列的前幾項是 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378…… 。從佩爾(Pell)數數列的第三項開始，任意一項與它相鄰前項的比值會趨近於$\sqrt{2}$+1。