平均成長率

平均壽命的平均成長率

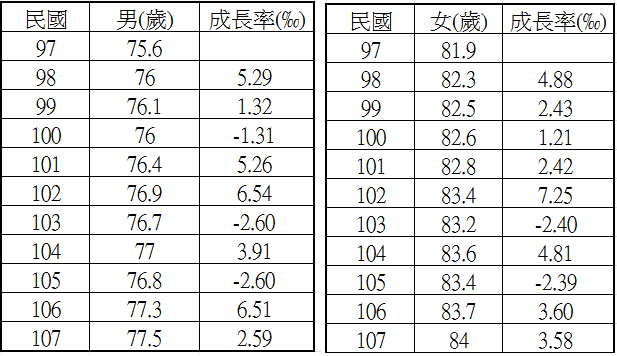
附表︰民國97年~民國107年，台灣兩性平均壽命

以女性為例，106年的平均壽命成長率是$\large\frac{83.7-83.4}{83.4}$=$\large\frac{83.7}{83.4}$-1≒0.0036=3.6(‰)。

107年的平均壽命成長率是$\large\frac{84-83.7}{83.7}$=$\large\frac{84}{83.7}$-1≒0.00358=3.58(‰)。

因為105年的平均壽命是83.4歲，可以計算107年的平均壽命=83.4×(1+3.6‰)×(1+3.58‰)≒84.0(歲)。

民國98年~民國107年的女性的平均壽命的成長率分別是4.88‰、2.43‰、1.21‰、2.42‰、7.25‰、-2.4‰、4.81‰、-2.39‰、3.60‰、3.58‰。如何計算這10年的女性平均壽命的平均成長率?

原來，81.9×(1+4.88‰)×(1+2.43‰)×(1+1.21‰)×(1+2.42‰)×(1+7.25‰)×(1-2.40‰)×(1+4.81‰)×(1-2.39‰)×(1+3.60‰)×(1+3.58‰)≒84.0 (歲)。...(1)
假設這10年的女性的平均壽命的平均成長率是 r ，則
(1+r)¹⁰=
(1+4.88‰)×(1+2.43‰)×(1+1.21‰)×(1+2.42‰)×(1+7.25‰)×(1-2.40‰)×(1+4.81‰)×(1-2.39‰)×(1+3.60‰)×(1+3.58‰)。
因此1+r=
$\small\sqrt[10]{(1+4.88‰)(1+2.43‰)(1+1.21‰)(1+2.42‰)(1+7.25‰)(1-2.40‰)(1+4.81‰)(1-2.39‰)(1+3.60‰)(1+3.58‰)}$

=$\small\sqrt[10]{1.025638392}$=1.002534731，所以r=0.002534731≒2.535‰ 。
簡潔的算法如下，
81.9×(1+r)¹⁰=84，1+r=$\large\sqrt[10]{\frac{84}{81.9}}$=1.0025350，r=0.0025350≒2.535‰ ，所以女性平均壽命的平均成長率約2.535‰ 。...(2)

平時經常會誤解求平均數就是求算術平均數，例如︰求上山、下山的平均速率，經常誤解為上山速率和下山速率的算術平均數。其實正確解是上山速率和下山速率的調和平均數。

假設10年的成長率分別是r₁、r₂、r₃、r₄、r₅、r₆、r₇、r₈、r₉、r₁₀，且平均成長率是 r。則

1+r=$\small\sqrt[10]{(1+r_1)(1+r_2)(1+r_3)(1+r_4)(1+r_5)(1+r_6)(1+r_7)(1+r_8)(1+r_9)(1+r_{10})}$ ，也就是說︰
1+r是1+r₁、1+r₂、1+r₃、1+r₄、1+r₅、1+r₆、1+r₇、1+r₈、1+r₉、1+r₁₀的幾何平均數。
不過，還是有人"誤解"作 1+r = $\frac{(1+r_1)+(1+r_2)+(1+r_3)+(1+r_4)+(1+r_5)+(1+r_6)+(1+r_7)+(1+r_8)+(1+r_9)+(1+r_{10})}{10}$。

但是，如果 0<r<1，0<r_n<1，n=1~10，而且它們的數值都非常的小，則
(1+r₁)(1+r₂)(1+r₃)(1+r₄)(1+r₅)(1+r₆)(1+r₇)(1+r₈ )(1+r9)(1+r₁₀)≒1+(r₁+r₂+r₃+r₄+r₅+r₆+r₇+r₈+r₉+r₁₀)，且(1+r)¹⁰≒ 1+10r。
因此1+(r₁+r₂+r₃+r₄+r₅+r₆+r₇+r₈+r₉+r₁₀) ≒ 1+10r，得 r ≒ $\large\frac{(r_1+r_2+r_3+r_4+r_5+r_6+r_7+r_8+r_9+r_{10})}{10}$。

以附表為例，因為成長率都非常的小，大約是0.003，所以(1+4.88‰)×(1+2.43‰)×(1+1.21‰)×(1+2.42‰)×(1+7.25‰)×(1-2.40‰)×(1+4.81‰)×(1-2.39‰)×(1+3.60‰)×(1+3.58‰)≒1+(4.88+2.43+1.21+2.42+7.25-2.40+4.81-2.39+3.60+3.58)‰ = 1+25.39‰ ，81.9× (1+25.39‰)=83.98(歲) ，83.98(歲)和(1)準確值84.0 (歲)非常接近。

如果平均成長率是r且「r值非常的小」，則(1+r)¹⁰≒ 1+10r。因為(1+r)¹⁰ =(1+4.88‰)×(1+2.43‰)×(1+1.21‰)×(1+2.42‰)×(1+7.25‰)×(1-2.40‰)×(1+4.81‰)×(1-2.39‰)×(1+3.60‰)×(1+3.58‰)，所以
1+10r ≒ 1+(4.88+2.43+1.21+2.42+7.25-2.40+4.81-2.39+3.60+3.58)‰，得

r≒$\large\frac{4.88+2.43+1.21+2.42+7.25-2.40+4.81-2.39+3.60+3.58}{10}$‰=2.539‰，2.539‰和(2)平均成長率的準確值2.535‰是非常的接近。