| 作者 |
標題: 升高中資優班考試考古題_不等式 |
| 愛數學 |
 發表於: 2017/7/2 下午 09:14:13 發表於: 2017/7/2 下午 09:14:13

中一中數資班一題:
已知a,b,c皆為正整數,且a>1,若一元二次方程式ax^2+bx+c=0的兩根之絕對值皆大於1,則
abc(三數之乘積)之最小值為?
只推到兩根皆小於-1,a-b+c>0,就不知道怎麼往下寫了,請問該怎麼解?
|
| 3 |
 回覆於: 2017/7/3 上午 12:07:47 回覆於: 2017/7/3 上午 12:07:47

這題我半年前有做過 不過有點忘記解法了
記得是先把一些不等式列一列
最後在一個一個討論(a,b,c)的值有沒有可能發生
|
| Superman |
 回覆於: 2017/7/4 下午 08:56:49 回覆於: 2017/7/4 下午 08:56:49

最小的 a=2。
再接你知道的兩根都小於-1,考慮b。
若 b=4 不合
最小的 b=5。
再來考慮 c=1,2,3,
因為 2x^2+5x+c=0 在 [-1,0) 有一根 。
所以 取c=4 。
2*5*4=40
|
| Supernan |
 回覆於: 2017/7/4 下午 09:07:34 回覆於: 2017/7/4 下午 09:07:34

如果兩根有限制只能是實根的話
a=2
b=7
c=6
。
|
| Superman |
 回覆於: 2017/7/4 下午 09:11:57 回覆於: 2017/7/4 下午 09:11:57

我上面第一篇考慮有錯,不用理會。
|
| 愛數學 |
 回覆於: 2017/7/5 上午 10:56:47 回覆於: 2017/7/5 上午 10:56:47

謝謝你!
|
| yani |
 回覆於: 2017/7/7 下午 07:45:00 回覆於: 2017/7/7 下午 07:45:00

兩根為:[-b-√(bb-4ac)]/2a≦ [-b+√(bb-4ac)]/2a≦-2
只需證明[-b+√(bb-4ac)]/2a≦-2
-b+√(bb-4ac) ≦-4a,b>=4a+√(bb-4ac)...(1)
√(bb-4ac) ≦-4a+b,bb-4ac≦16aa-8ab+bb
-4ac≦16aa-8ab,-c≦4a-2b,4a≧2b-c...(2)
令a=2,由(1),b≧4a+√(bb-4ac),b的最小值為4a(此時bb-4ac=0)
b=8,c=8,合於(2),a,b,c=2,8,8
方程式為2xx+8x+8=0,兩根為-2,-2,係數積為128
不完整之處,尚待補充。
|
| P |
 回覆於: 2017/7/8 上午 08:25:33 回覆於: 2017/7/8 上午 08:25:33


|
| P |
 回覆於: 2017/7/8 上午 08:28:45 回覆於: 2017/7/8 上午 08:28:45


|
| yes |
 回覆於: 2018/2/5 上午 07:20:09 回覆於: 2018/2/5 上午 07:20:09

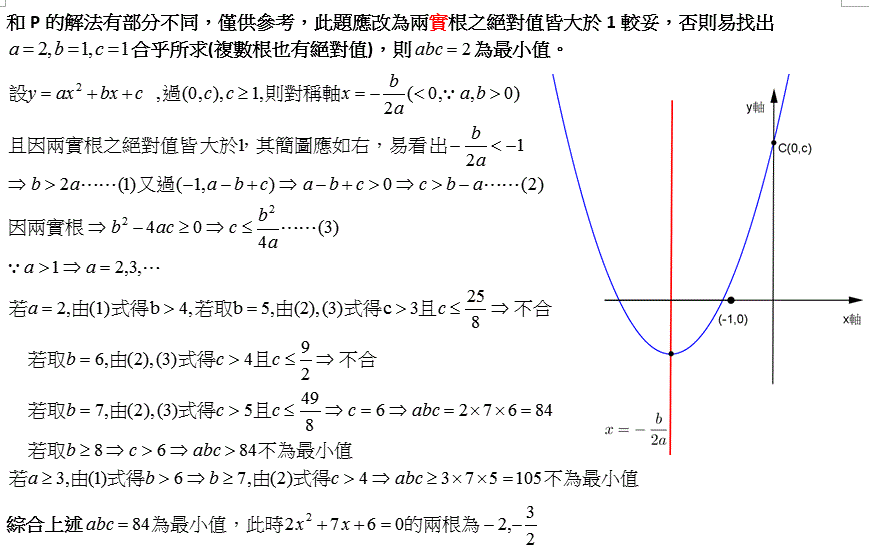
|

 升高中資優班考試考古題_不等式
升高中資優班考試考古題_不等式


 發表於: 2017/7/2 下午 09:14:13
發表於: 2017/7/2 下午 09:14:13

 回覆於: 2017/7/3 上午 12:07:47
回覆於: 2017/7/3 上午 12:07:47

