拉格朗日

拉格朗日（Joseph-Louis Lagrange，1736～1813）

拉格朗日於1736年1月25日生於義大利的杜林(Turin)，1756年接受法王路易十六的邀請定居巴黎，直至去世。通常被認定是法國數學家，名字LAGRANGE被刻印在巴黎艾菲爾鐵塔，表彰其對科學的貢獻。拉格朗日在數論以及分析力學和天體力學領域做出了重大貢獻。腓特烈大帝稱讚他是「歐洲最偉大的數學家」，拿破崙讚譽『拉格朗日是數學科學高聳的金字塔』

17歲時，讀了英國天文學家愛德蒙·哈雷(Edmond Halley)於1693 年關於代數在光學中的應用的著作，對於哈雷彗星可以週期性經過地球的週期計算法感到興趣。哈雷彗星每76.1年環繞太陽一週，用肉眼就可以看見。他也因杜林學院的貝卡里亞教授的出色教學而對物理學感興趣，並決定在數學領域成就一番事業。1755年，19歲的拉格朗日在尤拉的研究基礎上，以分析的方法求變分的極值。發表論文〈極大和極小的方法研究〉，關鍵定理是尤拉－拉格朗日方程式。它是一個二階偏微分方程式。它提供了求泛函的臨界點。在尋找函數的極大和極小值時，在一個解附近的微小變化的分析給出一階的一個近似。拉格朗日為變分法奠定理論基礎，變分法讓拉格朗日在杜林的名聲大為提升，並使他當上了杜林皇家炮兵學校的教授，成為當時歐洲的第一流數學家。1756年，尤拉推薦拉格朗日成為為柏林科學院院士。1766年，尤拉和達朗貝爾(d'Alembert) 一起推薦拉格朗日成為繼承尤拉在柏林科學院的首席地位。

1770年，拉格朗日發表四平方和定理：「任何非負整數可以四個整數的平方和表示」，例如：11＝0²+1²+1²+3²，23＝1²+2²+3²+3²。較早之前的1743年，尤拉也發現一個類似的恆等式，
(a²+b²+c²+d²)(x²+y²+z²+w²)=(ax+by+cz+dw)²+(ay-bx+cw-dz)²+(az-bw-cx+dy)²+(aw+bz-cy-dx)²，即兩個四平方和的乘積仍可以四平方和表示。

1786年腓特烈大帝去世以後，他接受了法王路易十六的邀請，離開柏林，定居巴黎。

拉格朗日開創拉格朗日力學，是分析力學中的一種，著重於數學解析的方法，對於古典力學用一種新的理論表述。 1788年發表他最重要的著作《分析機械》（Mécanique analytique），是分析力學後來發展工作的基礎。1790年，拉格朗日在法國科學院委員會負責標準化度量衡。他們研究公制，提倡長度、面積、體積和質量單位的十進位制。1799年法國完成全國度量衡工作，得助於拉格朗日的大力推動。

1794年，巴黎成立了兩所最高學府，巴黎高等師範學院和巴黎綜合理工大學。隔年，拉格朗日同時在這兩所大學任教。拉格朗日和蒙日（Gaspard Monge）同時成為巴黎綜合理工大學的首席數學教授。巴黎高等師範學院成立，旨在培訓學校教師。拉格朗日在那裡教授初等數學課程，編寫了《師範學校數學基礎教程》。知名數學家傅立葉當時就讀巴黎高等師範學院，是拉格朗日的學生。拉格朗日陸續在1797年演講〈Theory of Analytic Functions〉，1804年演講〈Lessons on the Calculus of Functions〉，並綜合整理成為第一本關於實解析函數的教科書。

拉格朗日插值法最早是英國數學家愛德華·華林(Edward Waring)於1779年發現。1795年，拉格朗日在其著作《師範學校數學基礎教程》中發表這個插值方法，此後就用他的名字來命名了。拉格朗日插值法是利用因式定理，以多項式來逼近函數。

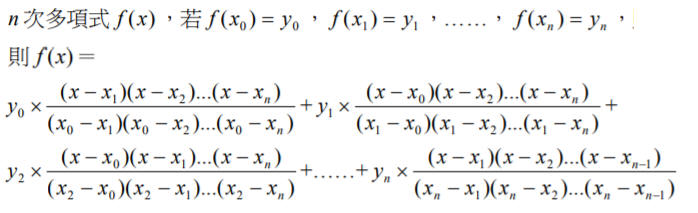
微積分以拉格朗日命名的重要定理，拉格朗日微分均值定理：

給定平面上固定兩端點的可微曲線，則這曲線在這兩端點間至少有一點，則過這點該曲線的切線斜率等於過兩端直線的斜率。

f:[a，b]→R，f在[a，b]是連續函數且f在(a，b)處處可微分，則在(a，b)存在c，使得$ f^{'} (c)$=$\large\frac{f(b)-f(a)}{b-a}$。

拉格朗日的名言

「一個人的貢獻和他的自負成強烈反比，這似乎是品行上的一個公理。」

「我把數學看成是一件有意義的工作，而不是想為自己建立紀念碑。」

1813年4月3日，拿破崙頒授帝國大十字勳章給拉格朗日，但此時的拉格朗日已臥病不起，於4月11日早晨，走完他輝煌的一生，享年77歲。

參考資料

Joseph-Louis Lagrange (1736 - 1813) - Biography - MacTutor History of Mathematics (st-andrews.ac.uk)