 笛卡兒誕生在法國一個富有的律師家庭,幼年曾被母親傳染肺結核病,身體虛弱經常無法到學校上課,只能臥病在床自學,以致有了獨自思考的習慣。
笛卡兒誕生在法國一個富有的律師家庭,幼年曾被母親傳染肺結核病,身體虛弱經常無法到學校上課,只能臥病在床自學,以致有了獨自思考的習慣。笛卡兒 (R'ene Descartes,1596–1650)
 笛卡兒誕生在法國一個富有的律師家庭,幼年曾被母親傳染肺結核病,身體虛弱經常無法到學校上課,只能臥病在床自學,以致有了獨自思考的習慣。
笛卡兒誕生在法國一個富有的律師家庭,幼年曾被母親傳染肺結核病,身體虛弱經常無法到學校上課,只能臥病在床自學,以致有了獨自思考的習慣。
1607年在法國 Anjou省的拉弗萊什(La Flèche) 寄宿在耶穌會學院受教育。在這裡他開始研讀德國天文 克拉維烏斯(Christopher Clavius)的數學著作,學習算術和幾何。
1613年在法國普瓦捷(Poityers)大學學習法律,1616年畢業。1618年在荷蘭的布雷達(Breda)就讀軍事學校學習軍事工程,同時在荷蘭科學家艾薩克·貝克曼(Isaac Beeckman)的指導下學習數學和物理力學。1620年離開軍旅生活。1618年在布雷達(Breda)逛街時看見佈告欄上貼著一道數學徵答難題,他竟然能夠解出正確答案。從此對數學有產生信心並下定決心研究。當時在他身邊幫忙翻譯的人,就是大他八歲的艾薩克·貝克曼,貝克曼在數學和物理學各方面都有很高的造詣,可說是笛卡耳在學術研究上的導師。
從 1620 年到 1628 年,笛卡兒遊歷歐洲,到過波希米亞、匈牙利、德國、荷蘭、法國、瑞士、義大利。 1623 年在巴黎和博學家 馬林·梅森 (Marin Mersenne)討論數論 和幾何學 家克勞德·邁多爾熱 (Claude Mydorge)討論圓錐曲線, 並保持了多年的聯繫。1628年笛卡兒厭倦了巴黎的喧囂,不再眷戀以前的旅行生活,決定在可以獨自研究的地方安頓下來。他選擇了荷蘭,在接下來的二十年裡,他似乎並不後悔。只有告訴梅森他住在哪裡,以便可以與數學世界保持聯繫,除此之外,他一直對於住處保密。
定居荷蘭後,1629 年至 1633 年期間 笛卡兒馬上撰寫第一部物理著作《世界論》(The Word) ,內文幾乎含蓋了他的哲學的完整版本,從方法到形而上學,再到物理學和生物學。可惜的是,因為伽利略被軟禁,所以到笛卡兒死後才出版《世界論》。
1637年發表《方法論》(Discourse on the Method),該書有一句著名的名言「我思,故我在」。書後有三個附錄包括《幾何學》( La Géométrie ),對於後來的解析幾何的發展產生重大的影響。
《幾何學》有三卷,第一卷討論尺規作圖,他改良了韋達的符號系統,視 a、b、c為已知數,首次引進 x、y、z當作未知數。首創直角坐標平面,並將點坐標化。
第二卷是曲線的性質,利用代數的方法求曲線的切線。
第三卷是立體和超立體的作圖,它實際上是討論方程式的根的性質。
他為了讓幾何有一定的思考方法,創造坐標幾何。引進點坐標後,幾何圖形可以坐標化,幾何問題就成為解方程式的問題。笛卡兒坐標平面由正交的x軸和y軸構成,將曲線代數化,引入變數導出動點的軌跡方程式,並利用解方程組來求不同曲線的交點。
古希臘幾何以圖形為主,把曲線分為立體曲線、平面曲線、線性曲線三種。立體曲線即圓錐曲線,平面曲線即能以尺規作圖的圖形,此外皆視為線性曲線,而線性曲線被認為不能登大雅之堂。但是笛卡兒不同意古希臘人對線性曲線的觀點,他的解析幾何,賦予幾何曲線更寬廣的空間,他用x、y的有限次方的方程式來表示曲線,創造出一個全新的數學領域--解析幾何。解析幾何對於後來的萊布尼茲和牛頓的微積分影響鉅大。
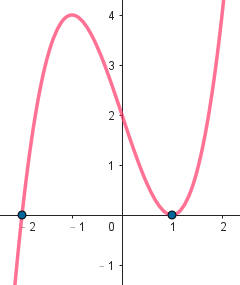
笛卡兒在他的作品《幾何學》(La Géométrie)首次提出笛卡兒符號法則,這是一個用於確定多項式方程式的正根或負根的個數的方法。如果把一元實係數多項式f(x)按降冪排列,則f(x)=0的正根的個數等於相鄰非零係數的符號的變化次數,或者比它依次小2的整倍數。如果相鄰非零係數的符號的變化次數是n,則正根個數是 n 或 n-2 或 n-4..。例如 x3-3x+2=0非零係數的符號的變化次數是2,則正根有2個,負根有1個,如附圖。
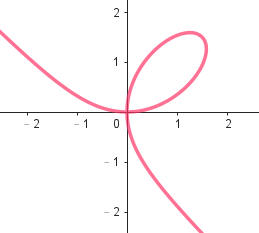
笛卡兒在1638年首先提出葉形線,x3+y3-3xy=0在直角坐標平面的圖形就是葉形線。如附圖
1860年從笛卡兒的一本筆記發現他早在1635年就已經證明 V-E+F=2,這是著名的尤拉公式,但是尤拉在1750年才證明它,比笛卡耳晚了一世紀,所以這個公式也稱作為尤拉-笛卡兒公式。
參考資料:
數學發展史---王懷權/著 (協進圖書公司)
阿草的葫蘆(下)---曹亮吉/著 (遠哲基金會)
René Descartes (1596 - 1650) - Biography - MacTutor History of Mathematics (st-andrews.ac.uk)
Copyright ©昌爸工作坊 all rights reserved.