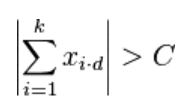 隨機投擲銅板,正面朝上記做+1,反面朝上記做-1,如果投擲非常多次,並記錄每一次的結果形成一個數列。
隨機投擲銅板,正面朝上記做+1,反面朝上記做-1,如果投擲非常多次,並記錄每一次的結果形成一個數列。艾狄胥差異問題
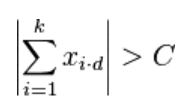 隨機投擲銅板,正面朝上記做+1,反面朝上記做-1,如果投擲非常多次,並記錄每一次的結果形成一個數列。
隨機投擲銅板,正面朝上記做+1,反面朝上記做-1,如果投擲非常多次,並記錄每一次的結果形成一個數列。
匈牙利數學家保羅.艾狄胥(Paul
Erdos)在西元1932年提出「the
Erdos Discrepancy Problem」的猜想,他認為可以在由+1與-1所形成的無窮數列,找到一個有限的子數列,該子數列的各項總和大於已知的常數C。
西元2014年2月,英國利物浦大學的計算機專家Alexei
Lisitsa博士和Boris
Konev博士利用電子計算機(電腦)證明了由+1與-1隨機組成且長度為1161的數列必定存在一個子數列,該子數列的各項總和大於2。電腦經過大約6小時的計算,包含證明細節的檔案大小大約是13Gb,比起知名的維基百科網站的容量(大約10Gb)還多,以致非常難用人工來檢驗其準確性。這就衍生出問題:「電腦證明數學命題,但是資料量過於龐大,以至於無法由人工進行驗證,那麼這個證明是否算是正確呢?」可是在現實裡,電腦成為數學研究的工具已是大勢所趨,需要極大運算量的數學問題,大多數情況也只能靠電腦的幫忙,電腦正在擴展數學研究的方法,並延伸數學研究的範疇。過去,四色問題、E8結構、Fekete問題、Kepler猜想等著名數學難題,都是借助電腦來證明的。
 西元2015年9月18日,2006年菲爾茲獎得主、華裔數學家陶哲軒宣布破解了80年沒有解決的「艾狄胥差異問題(the
Erdos Discrepancy Problem)」,論文預印本已經發表在arXiv.org上。 「艾狄胥差異問題」由數學家保羅·艾狄胥(Paul
Erdős)在西元1932年提出:「在任意只由1和-1組成的無限數列中,能找到項與項間等距的有限子數列,使得這個子數列各項之和的絕對值大於一個任意大的常數C。」
西元2015年9月18日,2006年菲爾茲獎得主、華裔數學家陶哲軒宣布破解了80年沒有解決的「艾狄胥差異問題(the
Erdos Discrepancy Problem)」,論文預印本已經發表在arXiv.org上。 「艾狄胥差異問題」由數學家保羅·艾狄胥(Paul
Erdős)在西元1932年提出:「在任意只由1和-1組成的無限數列中,能找到項與項間等距的有限子數列,使得這個子數列各項之和的絕對值大於一個任意大的常數C。」
參考資料:
A STA Attack on the
Erdos Discrepancy Conjectur
On the multiplicative Erdős discrepancy problem
陶哲軒的部落格:「The logarithmically averaged Chowla and Elliott
conjectures for two-point correlations; the Erdos discrepancy problem」
http://www.nature.com/news/maths-whizz-solves-a-master-s-riddle-1.18441
Copyright ©昌爸工作坊 All Rights Reserved.